Question

在△ABC中，点M是AB的中点，N点分AC的比为AN：NC=1：2，BN与CM相交于E，设

AB

=

a

，

AC

=

b

，则向量

AE

=（　　）

• A、

  1

  3

  a

  +

  1

  2

  b

• B、

  1

  2

  a

  +

  2

  3

  b

• C、

  2

  5

  a

  +

  1

  5

  b

• D、

  3

  5

  a

  +

  4

  5

  b

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：由于B，E，N三点共线，又N点分AC的比为AN：NC=1：2，利用向量共线定理可得存在实数m使得

AE

=m

AB

+(1-m)

AN

=m

AB

+

1

3

(1-m)

AC

，同理可得

AE

=n

AC

+

1

2

(1-n)

AB

．再根据平面向量基本定理即可解出．

解答： 解：如图所示，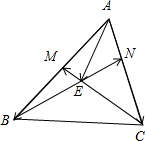
∵B，E，N三点共线，又N点分AC的比为AN：NC=1：2，
∴存在实数m使得

AE

=m

AB

+(1-m)

AN

=m

AB

+

1

3

(1-m)

AC

，
同理可得

AE

=n

AC

+

1

2

(1-n)

AB

．
根据平面向量基本定理可得：

m= 1 2 (1-n) 1 3 (1-m)=n

，解得

m= 2 5 n= 1 5

．
∴

AE

=

2

5

a

+

1

5

b

．
故选：C．

点评：本题考查了平面向量共线定理、平面向量基本定理，考查了推理能力和计算能力，属于中档题．