题目内容
7.f(x)=x2-2x+alnx.(Ⅰ)若a=2,求f(x)在点(1,f(1))处的切线方程;
(Ⅱ)讨论f(x)的单调性.
分析 (Ⅰ)当a=2时,f(x)=x2-2x+2lnx,求出导函数,求出切线的斜率,切点坐标,然后求解切线方程.
(Ⅱ)求出导函数$f'(x)=2x-2+\frac{a}{x}=\frac{{2{x^2}-2x+a}}{x}$(x>0),令h(x)=2x2-2x+a,通过△=4-8a,讨论$a≥\frac{1}{2}$时,a<$\frac{1}{2}$时,$0<a<\frac{1}{2}$时,a≤0时,导函数的符号,求解函数的单调区间即可.
解答 解:(Ⅰ)当a=2时,f(x)=x2-2x+2lnx,∴${f^'}(x)=2x-2+\frac{2}{x}$,
∴f'(1)=2,f(1)=-1,∴切线方程为y+1=2(x-1),即2x-y-3=0.
(Ⅱ)$f'(x)=2x-2+\frac{a}{x}=\frac{{2{x^2}-2x+a}}{x}$(x>0),
令h(x)=2x2-2x+a,△=4-8a,当△≤0,即$a≥\frac{1}{2}$时,f'(x)≥0,此时f(x)在定义域内单调递增;$当△>0,即a<\frac{1}{2}时,令h(x)=0,得{x_1}=\frac{{1-\sqrt{1-2a}}}{2},{x_2}=\frac{{1+\sqrt{1-2a}}}{2}$.
当$0<a<\frac{1}{2}$时,0<x<x1或x>x2时,f'(x)>0,f(x)单调递增;
x1<x<x2时,f'(x)<0,f(x)单调递减;
当a≤0时,0<x<x2时,f(x)单调递减,x>x2时,f(x)单调递增.
综上所述:$a≥\frac{1}{2}$时,f(x)在(0,+∞)上单调递增;$0<a<\frac{1}{2}$时,f(x)在$(0,\frac{{1-\sqrt{1-2a}}}{2})$,$(\frac{{1+\sqrt{1-2a}}}{2},+∞)$上单调递增,在$(\frac{{1-\sqrt{1-2a}}}{2},\frac{{1+\sqrt{1-2a}}}{2})$上单调递增;
a≤0时,f(x)在$(0,\frac{{1+\sqrt{1-2a}}}{2})$上单调递减,在$(\frac{{1+\sqrt{1-2a}}}{2},+∞)$上单调递增.
点评 本题画出函数的导数的应用,切线方程以及函数的单调区间的求法,考查分类讨论思想以及转化思想的应用,考查计算能力.

| A. | 是奇函数,且在(-∞,+∞)上是减函数 | B. | 是偶函数,且在(-∞,+∞)上是减函数 | ||
| C. | 是偶函数,且在(-∞,+∞)上是增函数 | D. | 是奇函数,且在(-∞,+∞)上是增函数 |
| A. | y=sinx | B. | y=sin2|x| | C. | y=-cos2x | D. | y=cos2x |
| A. | 12 | B. | 18 | C. | 24 | D. | 36 |
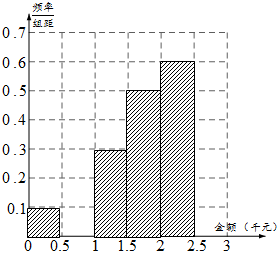 某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图):
某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图):| 网购金额 (单位千元) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
(1)试确定x,y,p,q的值,并补全频率分布直方图;
(2)试营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定5人,若需从这5人中随机选取2人进行问卷调查,则恰好选取1名“网购达人”和1名“非网购达人”的概率是多少?