题目内容

12．抛物线y2=2px（p＞0）的准线与圆x2+y2+2x=0相切，则p=4．

分析 求出抛物线的准线方程，圆的圆心坐标与半径，利用相切关系列出方程求解即可．

解答 解：抛物线y2=2px（p＞0）的准线方程为：x=-$\frac{p}{2}$；
圆x2+y2+2x=0的圆心（-1，0），半径为1，
抛物线的准线方程与圆相切可得：$-\frac{p}{2}=-2$，解得p=4．
故答案为：4．

点评 本题考查抛物线与圆的位置关系的应用，考查计算能力．

练习册系列答案
相关题目
2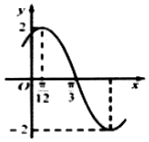．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，若将f（x）图象上所有点向右平移$\frac{π}{12}$个单位得到函数g（x）的图象，则函数g（x）的单调递减区间为（　　）
A．[kπ-$\frac{π}{3}$，kπ+$\frac{π}{6}$]，k∈ZB．[kπ+$\frac{π}{6}$，kπ+$\frac{2π}{3}$]，k∈Z
C．[kπ-$\frac{π}{12}$，kπ+$\frac{π}{12}$]，k∈ZD．[kπ-$\frac{7π}{12}$，kπ-$\frac{π}{12}$]，k∈Z
3．若采用系统抽样方法从420人中抽取21人做问卷调查，为此将他们随机编号为1，2，…，420，抽取的人的编号在区间[241，360]内的人数是（　　）
A．7B．6C．5D．8
20．已知$sinα+cosα=-\frac{{\sqrt{5}}}{2}$，且$\frac{5π}{4}＜α＜\frac{3π}{2}$，则cosα-sinα的值为（　　）
A．$-\frac{{\sqrt{3}}}{2}$B．$\frac{{\sqrt{3}}}{2}$C．$-\frac{3}{4}$D．$\frac{3}{4}$
7．f（x）=x2-2x+alnx．
（Ⅰ）若a=2，求f（x）在点（1，f（1））处的切线方程；
（Ⅱ）讨论f（x）的单调性．
17．若复数z满足z=1-2i，其中i为虚数单位，则复数z对应的点在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
4．在《我是歌手》的比赛中，有6位歌手（1～6号）进入决赛，在决赛中由现场的百家媒体投票选出最受欢迎的歌手，各家媒体独立地在投票器上选出3位候选人，其中媒体甲是1号歌手的歌迷，他必选1号，另在2号至6号中随机的选2名；媒体乙不欣赏2号歌手，他一定不选2号，；媒体丙对6位歌手的演唱没有偏爱，因此在1至6号歌手中随机的选出3名．
（1）求媒体甲选中5号且媒体乙未选中5号歌手的概率；
（2）ξ表示5号歌手得到媒体甲，乙，丙的票数之和，求ξ的分布列及数学期望．
1．已知函数f（x）=sin$\frac{π}{2}$x-1（x＜0），g（x）=logax（a＞0，且a≠1）．若它们的图象上存在关于y轴对称的点至少有3对，则实数a的取值范围是（　　）
A．（0，$\frac{\sqrt{5}}{5}$）B．（$\frac{\sqrt{5}}{5}$，1）C．（-∞，-1）D．（0，$\frac{\sqrt{3}}{3}$）
2．等差数列{an}的公差d＜0，且a${\;}_{1}^{2}$=a${\;}_{17}^{2}$，则数列{an}的前n项和Sn取得最大时的项数n是（　　）
A．8或9B．9或10C．10或11D．11或12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网