题目内容
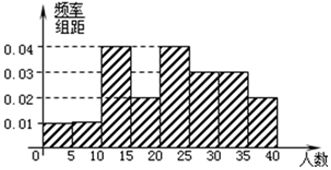
20．
2016年1月1日，我国实施“全面二孩”政策，中国社会科学院在某地随机抽取了150名已婚男性，其中愿意生育二孩的有100名，经统计，该100名男性的年龄情况对应的频率分布直方图如下：（1）根据频率分布直方图，估计这100名已婚男性的年龄平均值$\overline{x}$、众数、中位数和样本方差s2（同组数据用区间的中点值代替，结果精确到个位）；
（2）若在愿意生育二孩的且年龄在[30，34），[34，38），[38，42）的三组已婚男性中，用分层抽样的方法抽取19人，试估算每个年龄段应各抽取多少人？
分析 （1）由频率分布直方图即可计算得解．
（2）求出各个年龄段的频率，即可计算每个年龄段抽取的人数．
解答 （本题满分为12分）
解：（1）位已婚男性的年龄平均值$\overrightarrow{x}$和样本方差s2分别为：
$\overrightarrow{x}$=24×0.04+28×0.08+32×0.16+36×0.44+40×0.16+44×0.1+48×0.02=35.92≈36，…3分
s2=（-12）2×0.04+（-8）2+0.08+（-4）2×0.16+02×0.44+42×0.16+82×0.1+122×0.02=25.28≈25，…6分
可得：众数为36．…7 分；
中位数为（0.5-0.04-0.08-0.16）÷0.11+34=36，…9分
（2）在年龄段[30，34），[34，38），[38，42）的频率分别为0.04×4=0.16，0.11×4=0.44，0.04×4=0.16，0.16：0.44：0.16=4：11：4，
所以人数分别为4人，11人，4人…12分
点评 本题主要考查的考点有：1，频率分布直方图，2，中位数，众数，平均数及样本方差公式，关键是正确分析频率分布直方图的数据信息，准确计算．
练习册系列答案
相关题目
8．设曲线x=$\sqrt{2y-{y}^{2}}$上的点到直线x-y-2=0的距离的最大值为a，最小值为b，则a-b的值为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{2}}{2}$+1 | D． | 2 |
