题目内容
已知函数f(x)=
是奇函数,则sinα= .
|
考点:函数奇偶性的性质
专题:函数的性质及应用,三角函数的图像与性质
分析:由已知中函数f(x)=
是奇函数,可得cos(x+α)=sinx恒成立,进而α=-
+2kπ,k∈Z,进而可得sinα的值.
|
| π |
| 2 |
解答:
解:当x<0时,-x>0,
则f(x)=-x2+cos(x+α),f(-x)=(-x)2+sin(-x)=x2-sinx,
∵函数f(x)是奇函数,
∴f(-x)=-f(-x),
∴cos(x+α)=sinx恒成立,
∴α=-
+2kπ,k∈Z,
∴sinα=-1,
故答案为:-1
则f(x)=-x2+cos(x+α),f(-x)=(-x)2+sin(-x)=x2-sinx,
∵函数f(x)是奇函数,
∴f(-x)=-f(-x),
∴cos(x+α)=sinx恒成立,
∴α=-
| π |
| 2 |
∴sinα=-1,
故答案为:-1
点评:本题考查的知识点是函数奇偶性的性质,诱导公式,特殊角的三角函数值,是三角函数与函数图象和性质的综合应用,难度中档.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
已知集合A={x|lgx≤1},B={x|2x≤1},则A∪B等于( )
| A、(0,10] |
| B、(-∞,0] |
| C、(0,+∞) |
| D、(-∞,10] |
已知函数f(2x-1)=3x-4,则f(3)等于( )
| A、-3 | B、-4 | C、1 | D、2 |
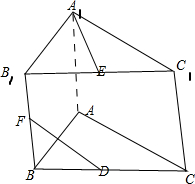 如图,在三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1垂直于底面,D、E分别为BC、B1C1的中点,F为侧棱BB1上的一点.
如图,在三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1垂直于底面,D、E分别为BC、B1C1的中点,F为侧棱BB1上的一点.