题目内容
16.学校举办了一次田径运动会,某班有8人参赛,后有举办了一次球类运动会,这个班有12人参赛,两次运动会都参赛的有3人,两次运动会中,这个班共有多少名同学参赛?( )| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
分析 设A为田径运动会参赛的学生的集合,B为球类运动会参赛的学生的集合,那么A∩B就是两次运动会都参赛的学生的集合,card(A),card(B),card(A∩B)是已知的,于是可以根据上面的公式求出card(A∪B).
解答 解:设A={x|x是参加田径运动会比赛的学生},B={x|x是参加球类运动会比赛的学生},
A∩B={x|x是两次运动会都参加比赛的学生},
A∪B={x|x是参加所有比赛的学生}.
因此card(A∪B)=card(A)+card(B)-card(A∩B)=8+12-3=17.
故两次运动会中,这个班共有17名同学参赛.
故选:A
点评 本题考查集合中元素个数的求法,是中档题,解题时要认真审题,注意公式card(A∪B)=card(A)+card(B)-card(A∩B)的合理运用.

练习册系列答案
相关题目
6.设复数z满足z(1+i)=|$\sqrt{3}$-i|(i是虚数单位),则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.F1、F2是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两焦点,Q是椭圆上任一点,过一焦点引∠F1QF2的外角平分线的垂线,则垂足M的轨迹为( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
6.已知偶函数f(x)在(0,+∞)上递减,已知a=0.2${\;}^{\sqrt{2}}$,b=log${\;}_{\sqrt{2}}$0.2,c=$\sqrt{2}$0.2,则f(a),f(b),f(c) 大小为( )
| A. | f(a)>f(b)>f(c) | B. | f(a)>f(c)>f(b) | C. | f(b)>f(a)>f(c) | D. | f(c)>f(a)>f(b) |
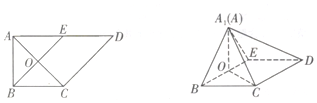 如图甲,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AD=2,AB=BC=1,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图乙
如图甲,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AD=2,AB=BC=1,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图乙