题目内容
7.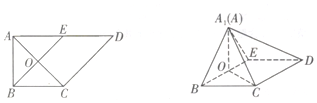 如图甲,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AD=2,AB=BC=1,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图乙
如图甲,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AD=2,AB=BC=1,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图乙(1)证明:CD⊥平面A1OC
(2)若平面A1BE⊥平面BCDE,求点B与平面A1CD的距离.
分析 (1)根据线面垂直的判定定理即可证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,利用等体积即可求点B与平面A1CD的距离.
解答 (1)证明:在图甲中,∵AB=BC=1,AD=2,E是AD的中点,∠BAD=$\frac{π}{2}$,
∴BE⊥AC,即在图乙中,BE⊥OA1,BE⊥OC.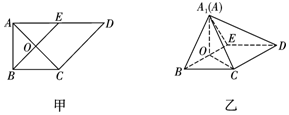
又OA1∩OC=O,∴BE⊥平面A1OC.
∵BC∥DE,BC=DE,
∴BCDE是平行四边形,
∴CD∥BE,∴CD⊥平面A1OC. …(6分)
(2)解:由题意,CD=BE=$\sqrt{2}$,平面A1BE⊥平面BCDE,
∴OA1⊥平面BCDE,∴OA1⊥OC
∴A1C=1
∵BE⊥平面A1OC,∴BE⊥A1C
∵CD∥BE,∴CD⊥A1C.
设B到平面A1CD的距离为d,
由$\frac{1}{3}×\frac{1}{2}×1×\sqrt{2}d=\frac{1}{3}×\frac{1}{2}×1×\frac{\sqrt{2}}{2}$,
∴d=$\frac{1}{2}$,故B到平面A1CD的距离为$\frac{1}{2}$ …(12分)
点评 本题考查了平面立体转化的问题,运用好折叠之前,之后的图形,对于空间直线平面的位置关系的定理要很熟练.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
17.命题p:抛物线x2=4y的焦点坐标为(0,1),q:“a=3”是“直线ax+2y=0与直线2x-3y=3垂直”的充要条件,则以下结论正确的是( )
| A. | p或q为真命题 | B. | p且q为假命题 | C. | p且¬q为真命题 | D. | ¬p或q为假命题 |
18.已知a,b是实数,则“a>1”是“a>2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
2.已知$a={({\frac{1}{3}})^x}$,b=x3,c=lnx,当x>2时,a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | c<b<a | D. | c<a<b |
12.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于P、Q两点,F2为右焦点,若△PQF2为等边三角形,则椭圆的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
19.己知命题p:“a>b”是“2a>2b”的充要条件;q:?x∈R,ex<lnx,则( )
| A. | ¬p∨q为真命题 | B. | p∧¬q为假命题 | C. | p∧q为真命题 | D. | p∨q为真命题 |
17.定义在$[{\frac{1}{π},π}]$上的函数f(x),满足$f(x)=f(\frac{1}{x})$,且当$x∈[{\frac{1}{π},1}]$时,f(x)=lnx,若函数g(x)=f(x)-ax在$[{\frac{1}{π},π}]$上有零点,则实数a的取值范围是( )
| A. | $[{-\frac{lnπ}{π},0}]$ | B. | [-πlnπ,0] | C. | $[{-\frac{1}{e},\frac{lnπ}{π}}]$ | D. | $[{-\frac{e}{2},-\frac{1}{π}}]$ |