题目内容
1.已知函数$f(x)=\frac{2}{{{3^x}+1}}+a(a∈R)$为奇函数,(1)求a的值;
(2)当0≤x≤1时,关于x的方程f(x)+1=t有解,求实数t的取值范围;
(3)解关于x的不等式f(x2-mx)≥f(2x-2m).
分析 (1)利用f(0)=0,即可求a的值;
(2)当0≤x≤1时,关于x的方程f(x)+1=t有解,求出函数的值域,即可求实数t的取值范围;
(3)利用函数的单调性,化不等式为具体不等式,分类讨论,即可解关于x的不等式f(x2-mx)≥f(2x-2m).
解答 解:(1)∵x∈R,∴f(0)=0,∴a=-1….(3分)
(2)∵$f(x)=\frac{2}{{{3^x}+1}}-1∴f(x)+1=\frac{2}{{{3^x}+1}}$,∵0≤x≤1,∴2≤3x+1≤4….(5分)
∴$\frac{1}{2}≤f(x)+1≤1$….(7分)∴$\frac{1}{2}≤t≤1$….(8分)
(3)$f(x)=\frac{2}{{{3^x}+1}}-1$在R上单调递减,….(9分)
f(x2-mx)≥f(2x-2m)x2-mx≤2x-2m….(10分)
x2-(m+2)x+2m≤0(x-2)(x-m)≤0….(11分)
①当m>2时,不等式的解集是{x|2≤x≤m}
②当m=2时,不等式的解集是{x|x=2}
③当m<2时,不等式的解集是{x|m≤x≤2}….(14分)
点评 本题考查奇函数的性质,考查函数的值域,考查学生解不等式的能力,正确转化是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于P、Q两点,F2为右焦点,若△PQF2为等边三角形,则椭圆的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
6.正方形ABCD中,E为BC的中点,向量$\overrightarrow{AE}$,$\overrightarrow{BD}$的夹角为θ,则cosθ=$-\frac{\sqrt{10}}{10}$.
13.复数2-3i的虚部为( )
| A. | 3 | B. | 3i | C. | -3 | D. | -3i |
11.下列命题中为真命题的是( )
| A. | 若x≠0,则x+$\frac{1}{x}$≥2 | |
| B. | 若直线x-ay=0与直线x-ay=0互相垂直,则a=1 | |
| C. | 命题:“若x2=1,则x=1或x=-1”的逆否命题为:“若x≠1,且x≠-1,则x2≠1” | |
| D. | 一个命题的否命题为真,则它的逆否命题一定为真 |
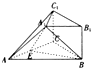 用如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.
用如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.