题目内容
13．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x＞0}\\{x+1，x≤0}\end{array}\right.$，则f（-2）=（ ）| A． | -1 | B． | 0 | C． | $\frac{1}{4}$ | D． | 4 |
分析 利用分段函数的性质即可得出．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x＞0}\\{x+1，x≤0}\end{array}\right.$，
∴f（-2）=-2+1=-1．
故选：A．
点评 本题考查了分段函数的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
4．已知双曲线$\frac{x^2}{16}-\frac{y^2}{b^2}=1，（b＞0）$实轴的一端点为A，虚轴的一端点为B，且|AB|=5，则该双曲线的方程为（ ）
| A． | $\frac{x^2}{16}-\frac{y^2}{15}=1$ | B． | $\frac{x^2}{16}-\frac{y^2}{12}=1$ | C． | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D． | $\frac{x^2}{16}-\frac{y^2}{3}=1$ |
1．对a，b∈R，记min{a，b}=$\left\{\begin{array}{l}{a，a≤b}\\{b，a＞b}\end{array}\right.$，函数f（x）=min{-|x|，-x2+4x+6}的最大值是（ ）
| A． | 6 | B． | 1 | C． | 0 | D． | $\frac{3-\sqrt{33}}{2}$ |
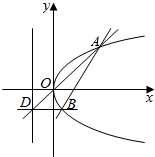已知斜率为1的直线l经过抛物线y2=2px（p＞0）的焦点F，且与抛物线相交于A，B两点，|AB|=4．