题目内容
在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)A(n):A1,A2,A3,…,An与B(n):B1,B2,B3,…,Bn,其中n≥3,若同时满足:①两点列的起点和终点分别相同;②线段AiAi+1⊥BiBi+1,其中i=1,2,3,…,n-1,则称A(n)与B(n)互为正交点列.
(Ⅰ)试判断A(3):A1(0,2),A2(3,0),A3(5,2)与B(3):B1(0,2),B2(2,5),B3(5,2)是否互为正交点列,并说明理由;
(Ⅱ)求证:A(4):A1(0,0),A2(3,1),A3(6,0),A4(9,1)不存在正交点列B(4);
(Ⅲ)是否存在无正交点列B(5)的有序整数点列A(5)?并证明你的结论.
(Ⅰ)试判断A(3):A1(0,2),A2(3,0),A3(5,2)与B(3):B1(0,2),B2(2,5),B3(5,2)是否互为正交点列,并说明理由;
(Ⅱ)求证:A(4):A1(0,0),A2(3,1),A3(6,0),A4(9,1)不存在正交点列B(4);
(Ⅲ)是否存在无正交点列B(5)的有序整数点列A(5)?并证明你的结论.
考点:进行简单的合情推理
专题:推理和证明
分析:(I)根据已知中中正交点列的定义,判断A(3):A1(0,2),A2(3,0),A3(5,2)与B(3):B1(0,2),B2(2,5),B3(5,2)是否满足条件,可得结论.
(II)点列B1,B2,B3,B4是点列A1,A2,A3,A4的正交点列,进而根据正交点列的定义,得到假设不成立,进而说明A(4):A1(0,0),A2(3,1),A3(6,0),A4(9,1)不存在正交点列B(4);
(Ⅲ)有序整点列B1,B2,B3,B4,B5是点列A1,A2,A3,A4,A5的正交点列,利用正交点列的定义,构造方程组,进而根据方程组有解得答案.
(II)点列B1,B2,B3,B4是点列A1,A2,A3,A4的正交点列,进而根据正交点列的定义,得到假设不成立,进而说明A(4):A1(0,0),A2(3,1),A3(6,0),A4(9,1)不存在正交点列B(4);
(Ⅲ)有序整点列B1,B2,B3,B4,B5是点列A1,A2,A3,A4,A5的正交点列,利用正交点列的定义,构造方程组,进而根据方程组有解得答案.
解答:
解:(Ⅰ)有序整点列A1(0,2),A2(3,0),A3(5,2)与B1(0,2),B2(2,5),B3(5,2)互为正交点列.-------------------------(1分)
理由如下:
由题设可知
=(3,-2),
=(2,2),
=(2,3),
=(3,-3),
因为
•
=0,
•
=0
所以 A1A2⊥B1B2,A2A3⊥B2B3.
所以整点列A1(0,2),A2(3,0),A3(5,2)与B1(0,2),B2(2,5),B3(5,2)互为正交点列.----------------------------(3分)
(Ⅱ)证明:由题意可得
=(3,1),
=(3,-1),
=(3,1),
设点列B1,B2,B3,B4是点列A1,A2,A3,A4的正交点列,
则可设
=λ1(-1,3),
=λ2(1,3),
=λ3(-1,3),λ1,λ2,λ3∈Z
因为A1与B1,A4与B4相同,所以有
因为λ1,λ2,λ3∈Z,方程②不成立,
所以有序整点列A1(0,0),A2(3,1),A3(6,0),A4(9,1)不存在正交点列.----------(8分)
(Ⅲ)存在无正交点列的整点列A(5).-------------------------------------------(9分)
当n=5时,设
=(ai,bi),ai,bi∈Z,其中ai,bi是一对互质整数,i=1,2,3,4
若有序整点列B1,B2,B3,B4,B5是点列A1,A2,A3,A4,A5的正交点列,
则
=λi(-bi,ai),i=1,2,3,4,由
=
得
取A1(0,0),ai=3,i=1,2,3,4,b1=2,b2=-1,b3=1,b4=-1
由于B1,B2,B3,B4,B5是整点列,所以有λi∈Z,i=1,2,3,4.
等式②中左边是3的倍数,右边等于1,等式不成立,
所以存在无正交点列的整点列A(5).-----------------------------------(13分)
理由如下:
由题设可知
| A1A2 |
| A2A3 |
| B1B2 |
| B2B3 |
因为
| A1A2 |
| B1B2 |
| A2A3 |
| B2B3 |
所以 A1A2⊥B1B2,A2A3⊥B2B3.
所以整点列A1(0,2),A2(3,0),A3(5,2)与B1(0,2),B2(2,5),B3(5,2)互为正交点列.----------------------------(3分)
(Ⅱ)证明:由题意可得
| A1A2 |
| A2A3 |
| A3A4 |
设点列B1,B2,B3,B4是点列A1,A2,A3,A4的正交点列,
则可设
| B1B2 |
| B2B3 |
| B3B4 |
因为A1与B1,A4与B4相同,所以有
|
因为λ1,λ2,λ3∈Z,方程②不成立,
所以有序整点列A1(0,0),A2(3,1),A3(6,0),A4(9,1)不存在正交点列.----------(8分)
(Ⅲ)存在无正交点列的整点列A(5).-------------------------------------------(9分)
当n=5时,设
| AiAi+1 |
若有序整点列B1,B2,B3,B4,B5是点列A1,A2,A3,A4,A5的正交点列,
则
| BiBi+1 |
| 4 |
 |
| i=1 |
| AiAi+1 |
| 4 |
 |
| i=1 |
| BiBi+1 |
得
|
取A1(0,0),ai=3,i=1,2,3,4,b1=2,b2=-1,b3=1,b4=-1
由于B1,B2,B3,B4,B5是整点列,所以有λi∈Z,i=1,2,3,4.
等式②中左边是3的倍数,右边等于1,等式不成立,
所以存在无正交点列的整点列A(5).-----------------------------------(13分)
点评:本题考查的知识点是向量垂直的充要条件,存在性问题,反证法,难度较大,运算量也比较大,属于难题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
圆
,(θ为参数)的圆心到直线
,(t为参数)的距离是( )
|
|
| A、1 | ||
B、
| ||
C、
| ||
| D、3 |
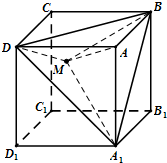 如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若f(M)=(
如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若f(M)=( 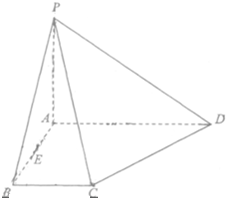 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,且∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD,E是线段AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,且∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD,E是线段AB的中点. 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为