题目内容
试判断函数f(x)=ex-x-3在区间[1,2]上是否有零点?
考点:函数零点的判定定理
专题:函数的性质及应用
分析:本题可以将原方程转化为两个函数的图象交点问题,利用根的存在性定理,可判断根的存在性,得到本题结论.
解答:
解:∵函数f(x)=ex-x-3,
∴令f(x)=0,
则有ex-x-3=0,
即ex=x+3.
记g(x)=ex,h(x)=x+3,
当x=1时,
g(1)=e1=e,h(1)=1+3=4,e≈2.718,
∴g(x)<h(x);
当x=2时,
g(2)=e2,h(2)=2+3=5,
e2≈7.39,
∴g(x)>h(x),
∴g(x)=h(x)在区间(1,2)内有交点.
∴函数f(x)=ex-x-3在区间[1,2]上一定有零点.
∴令f(x)=0,
则有ex-x-3=0,
即ex=x+3.
记g(x)=ex,h(x)=x+3,
当x=1时,
g(1)=e1=e,h(1)=1+3=4,e≈2.718,
∴g(x)<h(x);
当x=2时,
g(2)=e2,h(2)=2+3=5,
e2≈7.39,
∴g(x)>h(x),
∴g(x)=h(x)在区间(1,2)内有交点.
∴函数f(x)=ex-x-3在区间[1,2]上一定有零点.
点评:本题利用连续函数的图象研究方程的根,本题难度不大,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
设a=log
3,b=(
)0.3,c=lnπ,则( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、c<a<b |
| B、a<c<b |
| C、a<b<c |
| D、b<a<c |
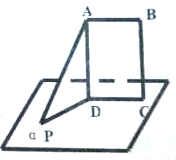 如图,已知AB∥α,AD⊥α,BC⊥α,垂足为D、C,PA⊥AB,求证:CD⊥平面PAD.
如图,已知AB∥α,AD⊥α,BC⊥α,垂足为D、C,PA⊥AB,求证:CD⊥平面PAD.