题目内容
已知
≤2x≤4,求函数f(x)=3+2×3x+1-9x的值域.
| 1 |
| 2 |
考点:二次函数在闭区间上的最值,函数的值域
专题:函数的性质及应用
分析:令t=2x,则
≤t≤4,g(t)=f(x)=-(t-3)2+12,再利用二次函数的性质求得它的值域.
| 1 |
| 2 |
解答:
解:令t=2x,则
≤t≤4,g(t)=f(x)=3+2×3x+1-9x=-t2+6t+3=-(t-3)2+12,
故当t=3时,函数f(x)取得最大值12,当t=
时,函数f(x)取得最小值为
,
故函数f(x)的值域为[
,12].
| 1 |
| 2 |
故当t=3时,函数f(x)取得最大值12,当t=
| 1 |
| 2 |
| 23 |
| 4 |
故函数f(x)的值域为[
| 23 |
| 4 |
点评:本题主要考查二次函数的性质的应用,体现了转化的数学思想,属基础题.

练习册系列答案
相关题目
给出下列四个命题:
①有理数是实数;
②有些平行四边形不是菱形;
③?x∈R,x2-2x>0;
④?x∈R,2x+1为奇数;
以上命题的否定为真命题的序号依次是 ( )
①有理数是实数;
②有些平行四边形不是菱形;
③?x∈R,x2-2x>0;
④?x∈R,2x+1为奇数;
以上命题的否定为真命题的序号依次是 ( )
| A、①④ | B、①②④ |
| C、①②③④ | D、③ |
已知两直线l1:(3+a)x+4y=5-3a与l2:2x+(5+a)y=8平行,则a=( )
| A、-7 | B、-1 |
| C、-7或-1 | D、7或1 |
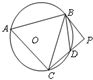 如图,PB为△ABC外接圆O的切线,BD平分∠PBC,交圆O于D,C,D,P共线.若AB⊥BD,PC⊥PB,PD=1,则圆O的半径是
如图,PB为△ABC外接圆O的切线,BD平分∠PBC,交圆O于D,C,D,P共线.若AB⊥BD,PC⊥PB,PD=1,则圆O的半径是