题目内容
求函数f(x)=x2+2x+a-1在区间(-∞,
]上的零点.
| 1 |
| 2 |
考点:函数的零点
专题:函数的性质及应用
分析:先求出f(x)的最小值,通过讨论a的范围,结合二次函数的性质,从而得到函数零点的个数.
解答:
解:∵f(x)=(x+1)2+a-2,对称轴x=-1,
∴f(x)在(-∞,-1)递减,在(-1,
]递增,
∴f(x)min=a-2,
当a-2>0,即a>2时,f(x)无零点,
当a-2=0,即a=2时,f(x)与x轴有1个交点(-1,0),
当a-2<0,即a<2时,令f(x)=0,解得x=-1±
,
令-1+
>
,解得:a<-
,
∴a<-
时,f(x)与x轴有1个交点(-1-
,0),
-
≤a<2时,f(x)与x轴有2个交点(-1-
,0),(-1+
,0),
综上,a>0时,函数f(x)无零点,
a=2时,函数f(x)有一个零点x=-1,
-
≤a<2时,函数f(x)有2个零点x=-1±
,
a<-
时,函数f(x)有1个零点x=-1-
.
∴f(x)在(-∞,-1)递减,在(-1,
| 1 |
| 2 |
∴f(x)min=a-2,
当a-2>0,即a>2时,f(x)无零点,
当a-2=0,即a=2时,f(x)与x轴有1个交点(-1,0),
当a-2<0,即a<2时,令f(x)=0,解得x=-1±
| 2-a |
令-1+
| 2-a |
| 1 |
| 2 |
| 1 |
| 4 |
∴a<-
| 1 |
| 4 |
| 2-a |
-
| 1 |
| 4 |
| 2-a |
| 2-a |
综上,a>0时,函数f(x)无零点,
a=2时,函数f(x)有一个零点x=-1,
-
| 1 |
| 4 |
| 2-a |
a<-
| 1 |
| 4 |
| 2-a |
点评:本题考查了函数的零点问题,考查了二次函数的性质,考查了分类讨论思想,是一道中档题.

练习册系列答案
相关题目
已知点A(1,
),B(-1,3
),则直线AB的倾斜角是( )
| 3 |
| 3 |
| A、60° | B、30° |
| C、120° | D、150° |
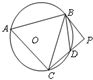 如图,PB为△ABC外接圆O的切线,BD平分∠PBC,交圆O于D,C,D,P共线.若AB⊥BD,PC⊥PB,PD=1,则圆O的半径是
如图,PB为△ABC外接圆O的切线,BD平分∠PBC,交圆O于D,C,D,P共线.若AB⊥BD,PC⊥PB,PD=1,则圆O的半径是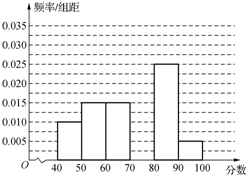 从参加高二年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
从参加高二年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: