题目内容
有限集合的元素可以一一数出来,无限集合的元素虽然不能数尽,但是可以比较两个集合元素个数的多少,例如,对于集合A={1,2,3,…,n,…}与B={2,4,6,…,2n,…},我们可以设计一种方法得出A与B的元素个数一样多的结论,类似地,给出下列4组集合:
(1)A={1,2,3,…,n,…}与B={2,4,8,…,2n,…}
(2)A=[0,1]与B=[0,2]
(3)A=(0,2]与B=[-1,+∞)
(4)A={(x,y)|x2+y2=1}与B={(x,y)|
+y2=1}
元素个数一样多的有( )
(1)A={1,2,3,…,n,…}与B={2,4,8,…,2n,…}
(2)A=[0,1]与B=[0,2]
(3)A=(0,2]与B=[-1,+∞)
(4)A={(x,y)|x2+y2=1}与B={(x,y)|
| x2 |
| 4 |
元素个数一样多的有( )
| A、1组 | B、2组 | C、3组 | D、4组 |
考点:类比推理
专题:操作型,函数的性质及应用
分析:令x∈A,y=2x∈B,可判断(1);令x∈A,y=2x∈B,可判断(2);令x∈A,y=log
x∈B,可判断(3);令(x,y)∈A,
∈B,可判断(4);
| 1 |
| 2 |
|
解答:
解:(1)中A={1,2,3,…,n,…}与B={2,4,8,…,2n,…}={21,22,23,…,2n,…},
令x∈A,y=2x∈B,且A与B的元素一一对应,即A与B的元素个数一样多;
(2)A=[0,1]与B=[0,2],
令x∈A,y=2x∈B,且A与B的元素一一对应,即A与B的元素个数一样多;
(3)A=(0,2]与B=[-1,+∞),
令x∈A,y=log
x∈B,且A与B的元素一一对应,即A与B的元素个数一样多;
(4)A={(x,y)|x2+y2=1}与B={(x,y)|
+y2=1}
令(x,y)∈A,
∈B,且A与B的元素一一对应,即A与B的元素个数一样多;
故元素个数一样多的有4组,
故选:D
令x∈A,y=2x∈B,且A与B的元素一一对应,即A与B的元素个数一样多;
(2)A=[0,1]与B=[0,2],
令x∈A,y=2x∈B,且A与B的元素一一对应,即A与B的元素个数一样多;
(3)A=(0,2]与B=[-1,+∞),
令x∈A,y=log
| 1 |
| 2 |
(4)A={(x,y)|x2+y2=1}与B={(x,y)|
| x2 |
| 4 |
令(x,y)∈A,
|
故元素个数一样多的有4组,
故选:D
点评:本题考查的知识点是类比推理,映射的概念,其中找到A,B中元素的对应方式是解答的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
已知向量
=(-1,2),
=(x,4),且
∥
,则x的值为( )
| a |
| b |
| a |
| b |
| A、8 | B、2 | C、-2 | D、-8 |
双曲线
-
=1的离心率为( )
| x2 |
| 42 |
| y2 |
| 32 |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
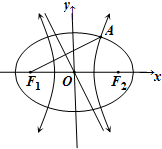 如图,F1,F2是椭圆C1:
如图,F1,F2是椭圆C1:| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 | ||
|
| 1 | ||
|
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
双曲线2x2-y2=8的虚轴长是( )
| A、2 | ||
B、2
| ||
| C、4 | ||
D、4
|
已知定义在(0,π)的函数 f(x)=sinx-
x,则f(x)的单调递减区间为( )
| 1 |
| 2 |
| A、(0,π) | ||
B、(0,
| ||
C、(
| ||
D、(
|