题目内容
14.抛物线y2=4x,直线l过焦点F,与其交于A,B两点,且$\overrightarrow{BA}=4\overrightarrow{BF}$,则△AOB(O为坐标原点)面积为$\frac{4\sqrt{3}}{3}$.分析 求出抛物线的焦点,设直线l为x=my+1,代入抛物线方程,运用韦达定理和向量的坐标表示,解得m,再由三角形的面积公式,计算即可得到.
解答 解:抛物线y2=4x的焦点为(1,0),
设直线l为x=my+1,代入抛物线方程可得,
y2-4my-4=0,
设A(x1,y1),B(x2,y2),
则y1+y2=4m,y1y2=-4,
由$\overrightarrow{BA}$=4$\overrightarrow{BF}$,可得y1=-3y2,
由代入法,可得m2=$\frac{1}{3}$,
又△AOB的面积为S=$\frac{1}{2}$|OF|•|y1-y2|=$\frac{1}{2}$$\sqrt{({{y}_{1}{+y}_{2})}^{2}-4{y}_{1}{y}_{2}}$=$\frac{1}{2}$$\sqrt{16{m}^{2}+16}$=$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{{4\sqrt{3}}}{3}$
点评 本题考查直线和抛物线的位置关系的综合应用,主要考查韦达定理和向量的共线的坐标表示,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.顶点在原点、坐标轴为对称轴的抛物线,过点(-1,2),则它的方程是( )
| A. | y=2x2或y2=-4x | B. | y2=-4x或x2=2y | C. | x2=-$\frac{1}{2}$y | D. | y2=-4x |
3.点P是抛物线y2=4x上一动点,则点P到点A(0,-1)的距离与到直线x=-1的距离和的最小值是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
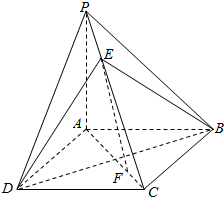 如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,点E、F在PC、AC上,PE=$\frac{1}{4}$PC.
如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,点E、F在PC、AC上,PE=$\frac{1}{4}$PC.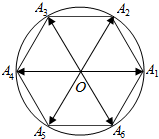 已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.
已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$. 如图,四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,且PD=AB=2.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,且PD=AB=2.