题目内容
17.设集合A={(x,y)|y=x+1},B={(x,y)||x|+|y|=1},则A∩B中的元素个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
分析 联立$\left\{\begin{array}{l}{y=x+1}\\{|x|+|y|=1}\end{array}\right.$,求出方程组的个数,即可判断元素的个数
解答 解:∵A={(x,y)|y=x+1},B={(x,y)||x|+|y|=1},
联立$\left\{\begin{array}{l}{y=x+1}\\{|x|+|y|=1}\end{array}\right.$,
当y>0时,可得的|x|+x+1=1,即|x|+x=0,此时x有无数个解,
即y=x+1,与|x|+|y|=1有无数个交点,
即A∩B中的元素个数为无数个.
故选:D
点评 本题考查了交集及其运算,考查了方程组的解法,是基础题.

练习册系列答案
相关题目
6.某工厂为了解用电量y与气温x℃之间的关系,随机统计了5天的用电量与当天气温,得到如下统计表:
$\sum_{i=1}^{5}$xiyi=5446,$\sum_{i=1}^{5}$xi2=4538,$\widehat{b}$=$\frac{\sum_{i=1}^{5}{x}_{i}{y}_{i}-5\overline{x}\overline{y}}{\sum_{i=1}^{5}{{x}_{i}}^{2}-5{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
(1)请根据表中的数据,求出y关于x的线性回归方程.据气象預报9月3日的平均气温是 23℃,请预测9月3日的用电量;(结果保留整数)
(2)请从表中任选两天,记用电量(万度)超过35的天数为ξ,求ξ的概率分布列,并求其数学期望和方差.
| 曰期 | 8月1曰 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
| 平均气温(℃) | 33 | 30 | 32 | 30 | 25 |
| 用电量(万度) | 38 | 35 | 41 | 36 | 30 |
(1)请根据表中的数据,求出y关于x的线性回归方程.据气象預报9月3日的平均气温是 23℃,请预测9月3日的用电量;(结果保留整数)
(2)请从表中任选两天,记用电量(万度)超过35的天数为ξ,求ξ的概率分布列,并求其数学期望和方差.
7.设A,B分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右顶点,P是双曲线C上异于A,B的任一点,设直线AP,BP的斜率分别为m,n,则$\frac{2a}{b}$+ln|m|+ln|n|取得最小值时,双曲线C的离心率为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{6}$ |
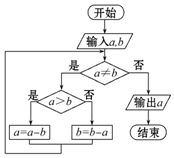 某同学根据“更相减损术”设计出程序框图(图).若输入a的值为98,b的值为63,则执行该程序框图输出的结果为( )
某同学根据“更相减损术”设计出程序框图(图).若输入a的值为98,b的值为63,则执行该程序框图输出的结果为( ) 在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图:
在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图: