题目内容
2.已知$\overrightarrow{AB}=(2,1)$,点C(-1,0),D(4,5),则向量$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为( )| A. | $\frac{{3\sqrt{2}}}{2}$ | B. | $-3\sqrt{5}$ | C. | $-\frac{{3\sqrt{5}}}{5}$ | D. | $3\sqrt{5}$ |
分析 运用向量的加减运算可得$\overrightarrow{CD}$=(5,5),运用向量的数量积的坐标表示,以及向量$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为$\frac{\overrightarrow{AB}•\overrightarrow{CD}}{|\overrightarrow{CD}|}$,即可得到所求值.
解答 解:$\overrightarrow{AB}=(2,1)$,点C(-1,0),D(4,5),
可得$\overrightarrow{CD}$=(5,5),
$\overrightarrow{AB}$•$\overrightarrow{CD}$=2×5+1×5=15,
|$\overrightarrow{CD}$|=5$\sqrt{2}$,
可得向量$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为:
$\frac{\overrightarrow{AB}•\overrightarrow{CD}}{|\overrightarrow{CD}|}$=$\frac{15}{5\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$.
故选:A.
点评 本题考查向量的数量积的坐标表示,以及向量的投影的概念,考查运算能力,属于基础题.

练习册系列答案
相关题目
12.若某空间几何体的三视图如图所示,则该几何体的表面积是( )
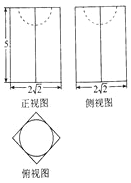

| A. | 48+π | B. | 48-π | C. | 48+2π | D. | 48-2π |
13.为迎接春节,某工厂大批生产小孩具--拼图,工厂为了规定工时定额,需要确定加工拼图所花费的时间,为此进行了10次试验,测得的数据如下:
(1)画出散点图,并判断y与x是否具有线性相关关系;
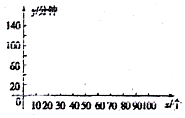
(2)求回归方程;
(3)根据求出的回归方程,预测加工2010个拼图需要用多少小时?(精确到0.1)
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y})}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}$$,\hat a=\bar y-\hat b\bar x$.
| 拼图数x/个 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y/分钟 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |

(2)求回归方程;
(3)根据求出的回归方程,预测加工2010个拼图需要用多少小时?(精确到0.1)
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y})}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}$$,\hat a=\bar y-\hat b\bar x$.
| 参考数据 | 合计 | ||||||||||
| x | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 550 |
| y | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 | 917 |
| xi2 | 100 | 400 | 900 | 1600 | 2500 | 3600 | 4900 | 6400 | 8100 | 10000 | 38500 |
| xiyi | 620 | 1360 | 2250 | 3240 | 4450 | 5700 | 7140 | 8840 | 10350 | 12200 | 55950 |
10.若实数a,b满足a>b且lna•lnb>0,则( )
| A. | loga2>logb2 | B. | a•lna>b•lnb | C. | 2ab+1>2a+b | D. | ab>ba |
11.某班有30名男生,20名女生,现要从中选出5人组成一个宣传小组,其中男、女学生均不少于2人的选法为( )
| A. | $C_{30}^2$$C_{20}^2$$C_{46}^1$ | |
| B. | $C_{50}^5-C_{30}^5-C_{20}^5$ | |
| C. | $C_{50}^5-C_{30}^1C_{20}^4-C_{30}^4C_{20}^1$ | |
| D. | $C_{30}^3C_{20}^2+C_{30}^2C_{20}^3$ |
 如图,平面内有三个向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,∠AOB=120°,∠AOC=45°,且|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=2$\sqrt{3}$,若$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,则λ+μ的值为$\sqrt{6}$+3$\sqrt{2}$.
如图,平面内有三个向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,∠AOB=120°,∠AOC=45°,且|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=2$\sqrt{3}$,若$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,则λ+μ的值为$\sqrt{6}$+3$\sqrt{2}$.