题目内容
12．若某空间几何体的三视图如图所示，则该几何体的表面积是（ ）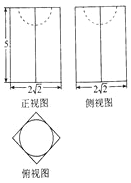
| A． | 48+π | B． | 48-π | C． | 48+2π | D． | 48-2π |
分析 由三视图还原原几何体，可得原几何体为底面边长是2，高是5的正四棱柱内部挖去一个半径为1的半球．然后利用正方体的表面积及球的表面积求解．
解答 解：由三视图可知，原几何体为底面边长是2，高是5的正四棱柱内部挖去一个半径为1的半球．
其表面积为$2×2×2+4×2×5-π×{1}^{2}+\frac{1}{2}×4π×{1}^{2}$=48+π．
故选：A．
点评 本题考查由三视图求几何体的表面积和体积问题，关键是由三视图还原原几何体，是中档题．
练习册系列答案
相关题目
19．复数z满足z（2+i）=3-6i（i为虚数单位），则复数z的虚部为（ ）
| A． | 3 | B． | -3 | C． | 3i | D． | -3i |
某湿地公园有一边长为4百米的正方形水域ABCD，如图，EF是其中轴线，水域正中央有一半径为1百米的圆形岛屿M，小岛上种植有各种花卉．现欲在线段AF上某点P处（AP的长度不超过1百米）开始建造一直线观光木桥与小岛边缘相切（不计木桥宽度），与BC相交于Q点．过Q点继续建造直线木桥NQ与小岛边缘相切，NQ与中轴线EF交于N点，N点与E点也以木桥直线相连．
7．已知O为原点，当θ=-$\frac{π}{6}$时，参数方程$\left\{\begin{array}{l}{x=3cosθ}\\{y=9sinθ}\end{array}\right.$（θ为参数）上的点为A，则直线OA的倾斜角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
1．已知集合A={x|x2+4≤5x，x∈R}，B={（x，y）|y=3x+2，x∈R}，则A∩B=（ ）
| A． | （2，4] | B． | （2，+∞） | C． | [2，4] | D． | ∅ |
2．已知$\overrightarrow{AB}=（2，1）$，点C（-1，0），D（4，5），则向量$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为（ ）
| A． | $\frac{{3\sqrt{2}}}{2}$ | B． | $-3\sqrt{5}$ | C． | $-\frac{{3\sqrt{5}}}{5}$ | D． | $3\sqrt{5}$ |