Question

12．如图，平面内有三个向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$，∠AOB=120°，∠AOC=45°，且|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，|$\overrightarrow{OC}$|=2$\sqrt{3}$，若$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$，则λ+μ的值为$\sqrt{6}$+3$\sqrt{2}$．

Answer 1

分析 建立坐标系，代入坐标运算，求出λ和μ即可．

解答 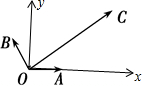解：以O为原点，以$\overrightarrow{OA}$为x轴建立坐标系，
则$\overrightarrow{OA}$=（1，0），$\overrightarrow{OB}$=（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），$\overrightarrow{OC}$=（$\sqrt{6}$，$\sqrt{6}$），
∵$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$，
∴$\left\{\begin{array}{l}{λ-\frac{1}{2}μ=\sqrt{6}}\\{\frac{\sqrt{3}}{2}μ=\sqrt{6}}\end{array}\right.$，解得λ=$\sqrt{6}$$+\sqrt{2}$，μ=2$\sqrt{2}$，
∴λ+μ=$\sqrt{6}$+3$\sqrt{2}$．
故答案为：$\sqrt{6}$+3$\sqrt{2}$．

点评 本题考查了平面向量的线性运算，属于基础题．