题目内容
已知△ABC的三个顶点A、B、C的坐标分别为(0,1)、(
,0)、(0,-2),O为坐标原点,动点P满足|
|=1,则|
+
+
|的最小值是 .
| 2 |
| CP |
| OA |
| OB |
| OP |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设点P(x,y),则由动点P满足|
|=1可得圆C:x2+(y+2)2=1.根据|
+
+
|=
,表示点P(x y)与点A(-
,-1)之间的距离.显然点A在圆C x2+(y+2)2=1的外部,求得AC的值,则AC-1即为所求.
| CP |
| OA |
| OB |
| OP |
(x+
|
| 2 |
解答:
解:设点P(x,y),则由动点P满足|
|=1可得 x2+(y+2)2=1.
根据
+
+
的坐标为(
+x,y+1),可得|
+
+
|=
,表示点P(x y)与点A(-
,-1)之间的距离.
显然点A在圆C x2+(y+2)2=1的外部,求得AC=
,|
+
+
|的最小值为AC-1=
-1,
故答案为:
-1.
| CP |
根据
| OA |
| OB |
| OP |
| 2 |
| OA |
| OB |
| OP |
(x+
|
| 2 |
显然点A在圆C x2+(y+2)2=1的外部,求得AC=
| 3 |
| OA |
| OB |
| OP |
| 3 |
故答案为:
| 3 |
点评:本题主要考查两点间的距离公式,两个向量坐标形式的运算,求向量的模,属于基础题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
下列函数在(0,+∞)上单调递增的是( )
| A、y=(x-1)2 | ||
| B、y=lg(x+3) | ||
| C、y=21-x | ||
D、y=
|
已知定义在(-1,1)上的函数f (x),其导函数为f′(x)=l+cosx,且f(0)=0,如果f(1-x)+f(l-x2)<0,则实数x的取值范围为( )
| A、(0,1) | ||||
B、(1,
| ||||
C、(-2,-
| ||||
D、(1,
|
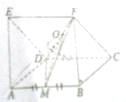 如图,在直三棱柱ADE-BCF中,面ABFE和面ABCD都是正方形且互相垂直,M为AB的中点,O为DF的中点,运动向量方法证明:
如图,在直三棱柱ADE-BCF中,面ABFE和面ABCD都是正方形且互相垂直,M为AB的中点,O为DF的中点,运动向量方法证明: