题目内容
18.已知命题p:函数f(x)=$\frac{{{{2017}^x}-1}}{{{{2017}^x}+1}}$是奇函数,命题q:函数g(x)=x3-x2在区间(0,+∞)上单调递增.则下列命题中为真命题的是( )| A. | p∨q | B. | p∧q | C. | ¬p∧q | D. | ¬p∨q |
分析 分别求出关于p,q的真假,求出复合命题的真假即可.
解答 解:f(-x)=$\frac{{2017}^{-x}-1}{{2017}^{-x}+1}$=$\frac{1{-2017}^{x}}{1{+2017}^{x}}$=-f(x),
故f(x)是奇函数,命题p是真命题;
g(x)=x3-x2,x∈(0,+∞),
g′(x)=3x2-2x=x(3x-2),
令g′(x)>0,解得:x>$\frac{2}{3}$,
令g′(x)<0,解得:0<x<$\frac{2}{3}$,
故g(x)在(0,$\frac{2}{3}$)递减,在($\frac{2}{3}$,+∞)递增,
故命题q是假命题;
故p∨q是真命题,p∧q是假命题,¬p∧q是假命题,¬p∨q是假命题,
故选:A.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,利用导数研究函数的单调性,函数的奇偶性等知识点,难度中档.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
8.已知复数z,满足z(2-i)=2+4i,则复数z等于( )
| A. | 2i | B. | -2i | C. | 2+i | D. | -2+i |
9.已知集合A={x∈R||x|≥2},B={x∈R|x2-x-2<0},则下列结论正确的是( )
| A. | A∪B=R | B. | A∩B≠∅ | C. | A∪B=∅ | D. | A∩B=∅ |
3.某理财公司有两种理财产品A和B.这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品A产品B(其中p、q>0)
(Ⅰ)已知甲、乙两人分别选择了产品A和产品B进行投资,如果一年后他们中至少有一人获利的概率大于$\frac{3}{5}$,求p的取值范围;
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品A和产品B之中选其一,应选用哪个?
产品A产品B(其中p、q>0)
| 投资结果 | 获利40% | 不赔不赚 | 亏损20% |
| 概 率 | $\frac{1}{3}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
| 投资结果 | 获利20% | 不赔不赚 | 亏损10% |
| 概 率 | p | $\frac{1}{3}$ |
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品A和产品B之中选其一,应选用哪个?
8.已知集合A={x|2x>1},B={x||x|<3},则A∩B=( )
| A. | (-3,0) | B. | (-3,3) | C. | (0,3) | D. | (0,+∞) |
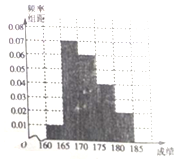 某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示:
某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示: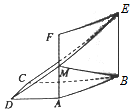 如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点,
如图所示,在直角梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD=2DC,四边形ABEF是正方形,且平面ABEF⊥平面ABCD,M为AF的中点, 如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.
如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.