题目内容
5.有1999个集合,每个集合有45个元素,任意两个集合的并集有89个元素,问此1999个集合的并集有多少个元素.分析 先确定任意两个集合有一个且只有一个共同的元素,再确定所有的共同元素都相等,即可得出结论.
解答 解:由题意,45+45-89=1,任意两个集合有一个且只有一个共同的元素.
假设集合A和B共同的元素是x,集合B和C共同的元素是y.
若x不等于y,则A和C共同的元素是另一个z 若z属于B,则AB和BC都有两个共同的元素,不成立
所以z不属于B,而这样的话,任意三个集合,他们两两的共同元素都不相同.
ABD三个集合中,BD共同的是w,这个w也不等于x ADE中,BE共同的是v,这个v也不等于x
以此类推,因为一共1999个集合,则除了AB还有1997,则会出现B和另一个集合的共同元素都不等于AB共同的x,而且有1997个,这显然和B只有45个元素矛盾
所以只能是AB共同的x和BC共同的y相等,
同理可得,所有的共同元素都相等,从而另外的44个都互不相等,
所以一共1999×44+1=87957个.
点评 本题考查并集及其运算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
15.设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下面的4个图形中,能表示集合M到集合N的函数关系的有( )
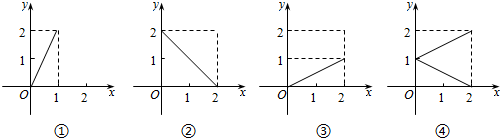
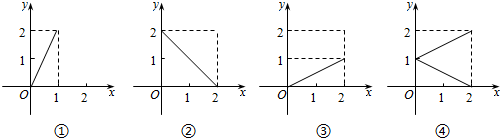
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
 如图数表,为一组等式:某学生根据上表猜测S2n-1=(2n-1)(an2+bn+c),老师回答正确,则a-b+c=5.
如图数表,为一组等式:某学生根据上表猜测S2n-1=(2n-1)(an2+bn+c),老师回答正确,则a-b+c=5.