题目内容
如果2lg(x-2y)=lgx+lgy,求lg
.
| x |
| y |
考点:对数的运算性质
专题:函数的性质及应用
分析:2lg(x-2y)=lgx+lgy,利用对数的运算性质可得(x-2y)2=xy,解出
并验证即可.
| x |
| y |
解答:
解:∵2lg(x-2y)=lgx+lgy,
∴lg(x-2y)2=lg(xy),
∴(x-2y)2=xy,
化为(
)2-5•
+4=0,解得
=1或4.
∵x>2y>0,
∴取
=4.
∴lg
=lg4=2lg2.
∴lg(x-2y)2=lg(xy),
∴(x-2y)2=xy,
化为(
| x |
| y |
| x |
| y |
| x |
| y |
∵x>2y>0,
∴取
| x |
| y |
∴lg
| x |
| y |
点评:本题考查了对数的运算性质,属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
抛物线y2=2x的准线方程是( )
A、x=-
| ||
| B、x=-1 | ||
C、y=-
| ||
| D、y=-1 |
若m,n是不同的直线,α,β是不同的平面,则下列命题中,错误的是( )
| A、若m⊥α,n⊥α,则m∥n |
| B、若m?α,α∥β,则m∥β |
| C、若m∥α,n∥α,则m∥n |
| D、若m∥n,m∥α,n?α,则n∥α |
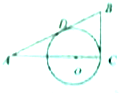 如图,AB和BC分别于圆O相切于点D,C,AC经过圆心O,且BC=2OC=4,则sinA=
如图,AB和BC分别于圆O相切于点D,C,AC经过圆心O,且BC=2OC=4,则sinA=