题目内容
已知实数a1，a2，a3，a4构成公差不为零的等差数列，且a1，a3，a4构成等比数列，则此等比数列的公比等于 ．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：利用实数a1，a2，a3，a4构成公差不为零的等差数列，且a1，a3，a4构成等比数列，确定a1=-4d，即可求出等比数列的公比．
解答：
解：∵a1，a3，a4构成等比数列，
∴a32=a1a4，
∴（a1+2d）2=a1（a1+3d），
∴a1=-4d，
∴q=
=
．
故答案为：
．
∴a32=a1a4，
∴（a1+2d）2=a1（a1+3d），
∴a1=-4d，
∴q=
| a3 |
| a1 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查等比数列的性质，考查等差数列的通项公式的运用，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
α≠
是sinα≠1的（ ）
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知命题p：?x0∈R，x02+ax0+a＜0．若命题p是假命题，则实数a的取值范围是（ ）
| A、[0，4] |
| B、（0，4） |
| C、（-∞，0）∪（4，+∞） |
| D、（-∞，0]∪[4，+∞） |
已知集合M={（x，y）|y2=x+1}，下列关系式中正确的是（ ）
| A、-1，0∈M |
| B、{-1，0}∈M |
| C、（-1，0）∈M |
| D、（-1，0）∉M |
与y=x为同一个函数的是（ ）
A、y=
| |||
B、y=
| |||
C、
| |||
D、y=(
|
i为虚数单位，（1-i）2=（ ）
| A、-2 i |
| B、2 i |
| C、1-2 i |
| D、2-2 i |
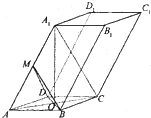已知四棱柱ABCD-A1B1C1D1的底面ABCD是边长为2的菱形，AC∩BD=O，AA1=2