题目内容
已知半圆C的参数方程为
,a为参数,a∈[-
,
].
(Ⅰ)在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,求半圆C的极坐标方程;
(Ⅱ)在(Ⅰ)的条件下,设T是半圆C上一点,且OT=
,试写出T点的极坐标.
|
| π |
| 2 |
| π |
| 2 |
(Ⅰ)在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,求半圆C的极坐标方程;
(Ⅱ)在(Ⅰ)的条件下,设T是半圆C上一点,且OT=
| 3 |
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:计算题,直线与圆,坐标系和参数方程
分析:(Ⅰ)运用平方法,可将半圆的参数方程化为普通方程,再由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,即可得到极坐标方程;
(Ⅱ)结合半圆的直径所对的圆周角为直角,再由特殊角的三角函数值,即可求得T点的极坐标.
(Ⅱ)结合半圆的直径所对的圆周角为直角,再由特殊角的三角函数值,即可求得T点的极坐标.
解答:
解:(Ⅰ)由半圆C的参数方程为
,a为参数,a∈[-
,
],
则圆的普通方程为x2+(y-1)2=1(0≤x≤1),
由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,
可得半圆C的极坐标方程为ρ=2sinθ,θ∈[0,
];
(Ⅱ)由题意可得半圆C的直径为2,设半圆的直径为OA,
则sin∠TAO=
,
由于∠TAO∈[0,
],则∠TAO=
,
由于∠TAO=∠TOX,
所以∠TOX=
,
T点的极坐标为(
,
).
|
| π |
| 2 |
| π |
| 2 |
则圆的普通方程为x2+(y-1)2=1(0≤x≤1),
由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,
可得半圆C的极坐标方程为ρ=2sinθ,θ∈[0,
| π |
| 2 |
(Ⅱ)由题意可得半圆C的直径为2,设半圆的直径为OA,
则sin∠TAO=
| ||
| 2 |
由于∠TAO∈[0,
| π |
| 2 |
| π |
| 3 |
由于∠TAO=∠TOX,
所以∠TOX=
| π |
| 3 |
T点的极坐标为(
| 3 |
| π |
| 3 |
点评:本题考查参数方程和普通方程以及极坐标方程的互化,考查圆的方程的运用,考查运算能力,属于基础题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
已知集合A={y∈Z|y=log2x,
<x≤8},B={x|
≥0},则A∩(∁RB)等于( )
| 1 |
| 2 |
| x+1 |
| x-2 |
| A、{0,1,2} |
| B、(-1,3] |
| C、{-1,0,1,2} |
| D、[-1,3) |
当掷五枚硬币时,已知至少出现两个正面向上,则正好出现3个正面向上的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
观察下列各式:32=9,33=27,34=81,…,则350末位数字为( )
| A、1 | B、3 | C、7 | D、9 |
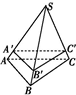 已知正棱锥S-ABC的底面边长为4,高为3,在正棱锥内任取一点P,使得VP-ABC<
已知正棱锥S-ABC的底面边长为4,高为3,在正棱锥内任取一点P,使得VP-ABC<| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|