题目内容
当掷五枚硬币时,已知至少出现两个正面向上,则正好出现3个正面向上的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:互斥事件的概率加法公式
专题:概率与统计
分析:本题是一个等可能事件的概率,先求出至少出现两个正面向上种数,再求出正好出现3个正面向上的种数,根据对立事件的概率公式得到结果
解答:
解:至少出现两个正面向上的种数为(所有的总数家去全是反面的和只有1个事正面向上的)25-1-5=26种,
正好出现3个正面向上,先排三个正面向上的,把两个反面插入所形成的4个间隔中,当两个反面的相邻时有
=4种,当两个反面的不相邻时有
=6种,故有4+6=10种,
故至少出现两个正面向上,则正好出现3个正面向上的概率为
=
,
故选:A.
正好出现3个正面向上,先排三个正面向上的,把两个反面插入所形成的4个间隔中,当两个反面的相邻时有
| C | 1 4 |
| C | 2 4 |
故至少出现两个正面向上,则正好出现3个正面向上的概率为
| 10 |
| 26 |
| 5 |
| 13 |
故选:A.
点评:本题考查古典概型以及排列组合及其概率计算公式的应用,体现了转化的数学思想,属于中档题

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
某学校高二年级共有学生180人,他们来自机电、电子、市场营销三个专业.为检查学生的学习情况,决定采用分层抽样的方法进行抽样,已知从机电、电子、市场营销三个专业抽取的个体数组成一个等差数列,则电子专业的学生人数为( )
| A、40 | B、60 | C、80 | D、120 |
已知函数f(x)=[ax2+(a-1)2x+a-(a-1)2]ex(其中a∈R).
(Ⅰ)若x=0为f(x)的极值点,求a的值;
(Ⅱ)在(Ⅰ)的条件下,解不等式f(x)>(x-1)(
x2+x+1).
(Ⅰ)若x=0为f(x)的极值点,求a的值;
(Ⅱ)在(Ⅰ)的条件下,解不等式f(x)>(x-1)(
| 1 |
| 2 |
已知向量
=(1,cosθ)与
=(2cosθ,1)平行,则cos2θ等于( )
| m |
| n |
| A、-1 | ||||
| B、0 | ||||
C、
| ||||
D、
|
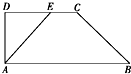 如图所示,在直角梯形ABCD中,AD⊥AB且AB=7,AD=3,CD=4,DE=3,若沿AE折起,使得平面ADE⊥平面ABCE,则四棱锥D-ABCE的外接球的体积为
如图所示,在直角梯形ABCD中,AD⊥AB且AB=7,AD=3,CD=4,DE=3,若沿AE折起,使得平面ADE⊥平面ABCE,则四棱锥D-ABCE的外接球的体积为 期末考试,教师阅卷评分,并检查每个学生成绩,如及格则作“升级”处理,不及格作“留级”处理.将下面的流程图补充完整.
期末考试,教师阅卷评分,并检查每个学生成绩,如及格则作“升级”处理,不及格作“留级”处理.将下面的流程图补充完整.