题目内容
已知函数f（x）=
+2x+1，其中f′（x）是f（x）的导函数，e为自然对数的底数，则f（x）在点（0，f（0））处的切线方程为 ．
| f′(0) |
| ex |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用,导数的综合应用
分析：求导f′（x）=-
+2；从而令x=0求f′（0）=1，再求切线方程．
| f′(0) |
| ex |
解答：
解：∵f（x）=
+2x+1，∴f′（x）=-
+2；
故f′（0）=-f′（0）+2；
故f′（0）=1；
f（0）=1+0+1=2；
故f（x）在点（0，f（0））处的切线方程为
y=x+2；
故切线方程为x-y+2=0．
故答案为：x-y+2=0．
| f′(0) |
| ex |
| f′(0) |
| ex |
故f′（0）=-f′（0）+2；
故f′（0）=1；
f（0）=1+0+1=2；
故f（x）在点（0，f（0））处的切线方程为
y=x+2；
故切线方程为x-y+2=0．
故答案为：x-y+2=0．
点评：本题考查了导数的综合应用及导数的几何意义的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
一个集合的所有真子集共有n个，则n不可能取以下哪个数（ ）
| A、0 | B、1 | C、2 | D、3 |
已知函数f（x）=[ax2+（a-1）2x+a-（a-1）2]ex（其中a∈R）．
（Ⅰ）若x=0为f（x）的极值点，求a的值；
（Ⅱ）在（Ⅰ）的条件下，解不等式f(x)＞(x-1)(
x2+x+1)．
（Ⅰ）若x=0为f（x）的极值点，求a的值；
（Ⅱ）在（Ⅰ）的条件下，解不等式f(x)＞(x-1)(
| 1 |
| 2 |
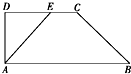如图所示，在直角梯形ABCD中，AD⊥AB且AB=7，AD=3，CD=4，DE=3，若沿AE折起，使得平面ADE⊥平面ABCE，则四棱锥D-ABCE的外接球的体积为
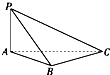如图所示的三棱锥P-ABC中，底面三角形ABC是边长为2的正三角形且PA=2，PA⊥底面ABC，求此三棱锥外接球的球心到侧面PAB的距离．已知f（x）是定义在R上的偶函数，g（x）是定义在R上的奇函数，且g（x）=f（x-1），则f（2015）的值为（ ）
| A、-1 | B、1 | C、0 | D、无法确定 |