题目内容
已知数列{ a n}的各项都是正数,且满足:a0=1,an+1=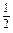 an·(4-an)(n∈N).
an·(4-an)(n∈N).
证明:an<an+1<2(n∈N).
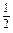 an·(4-an)(n∈N).
an·(4-an)(n∈N).证明:an<an+1<2(n∈N).
证明略
证明 方法一 用数学归纳法证明:
(1)当n=0时,a0=1,a1=
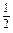 a0(4-a0)=
a0(4-a0)= ,
,所以a0<a1<2,命题正确.
(2)假设n=k时命题成立,即ak-1<ak<2.
则当n=k+1时,ak-ak+1?
=
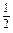 ak-1(4-ak-1)-
ak-1(4-ak-1)-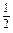 ak(4-ak)
ak(4-ak)=2(ak-1-ak)-
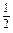 (ak-1-ak)(ak-1+ak)
(ak-1-ak)(ak-1+ak)=
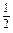 (ak-1-ak)(4-ak-1-ak).
(ak-1-ak)(4-ak-1-ak).而ak-1-ak<0,4-ak-1-ak>0,所以ak-ak+1<0.
又ak+1=
 ak(4-ak)=
ak(4-ak)= [4-(ak-2)2]<2.
[4-(ak-2)2]<2.所以n=k+1时命题成立.
由(1)(2)可知,对一切n∈N时有an<an+1<2.
方法二 用数学归纳法证明:
(1)当n=0时,a0=1,a1=
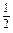 a0(4-a0)=
a0(4-a0)=  ,
,所以0<a0<a1<2;
(2)假设n=k时有ak-1<ak<2成立,
令f(x)=
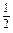 x(4-x),f(x)在[0,2]上单调递增,
x(4-x),f(x)在[0,2]上单调递增,所以由假设有:f(ak-1)<f(ak)<f(2),
即
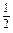 ak-1(4-ak-1)<
ak-1(4-ak-1)<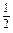 ak(4-ak)<
ak(4-ak)<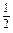 ×2×(4-2),
×2×(4-2),也即当n=k+1时,ak<ak+1<2成立.
所以对一切n∈N,有ak<ak+1<2.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
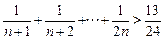 .
. ,观察下列不等式:
,观察下列不等式: ,
, ,…,请你猜测
,…,请你猜测 将满足的不等式,并用数学归纳法加以证明。
将满足的不等式,并用数学归纳法加以证明。 N*,1-
N*,1- +
+ -
- +…+
+…+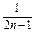 -
-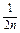 =
= +
+ +…+
+…+ 是完全平方数的正整数
是完全平方数的正整数 有 ( )
有 ( )
 ,且
,且 ,则
,则 的最小值为______.
的最小值为______. 最大值.
最大值.