题目内容
用数学归纳法证明:对任意的n N*,1-
N*,1- +
+ -
- +…+
+…+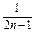 -
-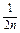 =
= +
+ +…+
+…+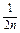 .
.
 N*,1-
N*,1- +
+ -
- +…+
+…+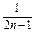 -
-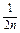 =
= +
+ +…+
+…+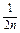 .
.证明略
证明 (1)当n=1时,左边=1- =
= =
= =右边,
=右边,
∴等式成立.
(2)假设当n=k(k≥1,k∈N*)时,等式成立,即
1- +
+ -
- +…+
+…+ -
- =
= +
+ +…+
+…+ .
.
则当n=k+1时,
1- +
+ -
- +…+
+…+ -
- +
+ -
-
= +
+ +…+
+…+ +
+ -
-
= +
+ +…+
+…+ +
+ +(
+( -
- )
)
= +
+ +…+
+…+ +
+ +
+ ,
,
即当n=k+1时,等式也成立,
所以由(1)(2)知对任意的n∈N*等式成立.
 =
= =
= =右边,
=右边,∴等式成立.
(2)假设当n=k(k≥1,k∈N*)时,等式成立,即
1-
 +
+ -
- +…+
+…+ -
- =
= +
+ +…+
+…+ .
.则当n=k+1时,
1-
 +
+ -
- +…+
+…+ -
- +
+ -
-
=
 +
+ +…+
+…+ +
+ -
-
=
 +
+ +…+
+…+ +
+ +(
+( -
- )
)=
 +
+ +…+
+…+ +
+ +
+ ,
,即当n=k+1时,等式也成立,
所以由(1)(2)知对任意的n∈N*等式成立.

练习册系列答案
相关题目
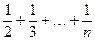 ,当n≥2,n
,当n≥2,n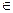 N*时,用数学归纳法证明:n+f(1)+f(2)+…+f(n-1)=nf(n)。
N*时,用数学归纳法证明:n+f(1)+f(2)+…+f(n-1)=nf(n)。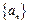 的前
的前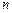 项和
项和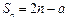 ,先计算数列的前4项,后猜想
,先计算数列的前4项,后猜想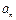 并证明之.
并证明之.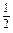 an·(4-an)(n∈N).
an·(4-an)(n∈N).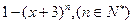 能被
能被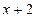 整除
整除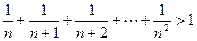 (
(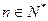 且
且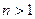 )
)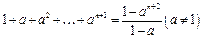 ,在验证
,在验证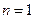 成立时,左边计算所得的项是
成立时,左边计算所得的项是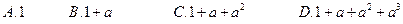
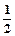 x2-1恒成立,求实数a的取值范围。
x2-1恒成立,求实数a的取值范围。