Question

在曲线y=cosx（

2

π

＜x＜

3π

2

）上有横坐标是x，x+

1

2

的A，B两点，它们在x轴上的射影是A′B′，则梯形A′ABB′的面积达到最大时，x的值为

 

．

Answer 1

考点：余弦函数的图象

专题：三角函数的图像与性质

分析：根据题意，求出A、B、A′、B′点的坐标，写出梯形A′ABB′的面积表达式，求出当面积取最大值时x的值．

解答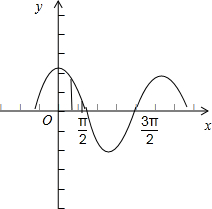： 解：如图所示，
∵y=cosx（

2

π

＜x＜

3π

2

），
∴A（x，cosx），B（x+

1

2

，cos（x+

1

2

））；
A′（x，0），B′（x+

1

2

，0）；
∴梯形A′ABB′的面积为
S=

1

2

|cosx+cos（x+

1

2

）|×（x+

1

2

-x）
=

1

4

|cosx+cos（x+

1

2

）|
=

1

4

×|2cos（x+

1

4

）cos

1

4

|
=

1

2

cos

1

4

|cos（x+

1

4

）|；
∵

2

π

＜x＜

3π

2

，
∴

2

π

+

1

4

＜x+

1

4

＜

3π

2

+

1

4

，
∴令x+

1

4

=π，得x=π-

1

4

；
∴当梯形A′ABB′的面积S达到最大时，
x的值为π-

1

4

．
故答案为：π-

1

4

点评：本题考查了三角函数的图象与性质的应用问题，解题时应建立函数模型，根据三角函数的有界性进行解答，是中档题．