Question

13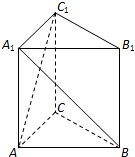．如图，三棱柱ABC-A₁B₁C₁中，AA₁⊥底面ABC，AC⊥AB且AA₁=AC=AB，则直线AC₁与直线A₁B所成的角等于（　　）

• A． 30°
• B． 45°
• C． 60°
• D． 90°

Answer 1

分析 如图所示，建立空间直角坐标系．利用向量夹角公式即可得出．

解答 解：如图所示，建立空间直角坐标系．
不妨设AB=1，则A（0，0，0），B（1，0，0），A₁（0，0，1），C₁（0，1，1），
∴$\overrightarrow{A{C}_{1}}$=（0，1，1），$\overrightarrow{B{A}_{1}}$=（-1，0，1），
∴$cos＜\overrightarrow{A{C}_{1}}，\overrightarrow{B{A}_{1}}＞$=$\frac{\overrightarrow{A{C}_{1}}•\overrightarrow{B{A}_{1}}}{|\overrightarrow{A{C}_{1}}||\overrightarrow{B{A}_{1}}|}$=$\frac{1}{\sqrt{2}×\sqrt{2}}$=$\frac{1}{2}$，
∴＜$\overrightarrow{A{C}_{1}}$，$\overrightarrow{B{A}_{1}}$＞=60^°，
∴异面直线AC₁与直线A₁B所成的角等于60^°．
故选：C．

点评 本题考查了异面直线所成的角、向量夹角公式、数量积运算性质，考查了推理能力与计算能力，属于中档题．