题目内容
4.已知y+5与3x+4成正比例,当x=1时,y=2.(1)求y与x的函数关系式;
(2)求当x=-1时的函数值.
分析 (1)由题意可得y+5=k(3x+4)(k≠0),分别代入x,y的值求得k,则y与x的函数关系式可求;
(2)直接在函数解析式中取x=-1求得y值.
解答 解:(1)由题意可得y+5=k(3x+4)(k≠0),
则2+5=k(3×1+4),解得k=1,
∴y=3x-1;
(2)当x=-1时,y=3×(-1)-1=-4.
点评 本题考查函数解析式的求解及常用方法,训练了利用待定系数法求函数解析式,是基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
14.已知某校5个学生的数学和物理成绩如表
(Ⅰ)假设在对这5名学生成绩进行统计时,把这5名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有2名学生的物理成绩是自己的实际分数的概率是多少?
(Ⅱ)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用x表示数学成绩,用y表示物理成绩,求y与x的回归方程;
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学xi | 80 | 75 | 70 | 65 | 60 |
| 物理yi | 70 | 66 | 68 | 64 | 62 |
(Ⅱ)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用x表示数学成绩,用y表示物理成绩,求y与x的回归方程;
参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
15.边长为4$\sqrt{3}$的等边△ABC中,D为边AB的中点,若P为线段CD的中点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的值为( )
| A. | 18 | B. | -18 | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
9.下列关于算法的说法中,正确的是( )
| A. | 算法是某个问题的解决过程 | B. | 算法执行后可以不产生确定的结果 | ||
| C. | 解决某类问题的算法不是唯一的 | D. | 算法可以无限的操作下去不停止 |
13.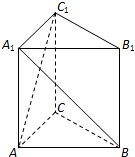 如图,三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥AB且AA1=AC=AB,则直线AC1与直线A1B所成的角等于( )
如图,三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥AB且AA1=AC=AB,则直线AC1与直线A1B所成的角等于( )
 如图,三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥AB且AA1=AC=AB,则直线AC1与直线A1B所成的角等于( )
如图,三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥AB且AA1=AC=AB,则直线AC1与直线A1B所成的角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
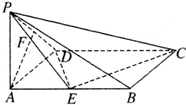 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB,PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E,F分别是AB,PD的中点. 在直三棱柱中,AA1=AB=BC=2,AC=1,D是AC中点.
在直三棱柱中,AA1=AB=BC=2,AC=1,D是AC中点.