题目内容
18.设集合A={0,a},集合B={a2,-a3,a2-1}且A⊆B,则a的值是1.分析 由A={0,a}及集合元素的互异性可知a≠0,所以a2≠0,-a3≠0,又A⊆B,所以a2-1=0,解得a=±1,再进行验证,即可得出结论.
解答 解:由A={0,a}及集合元素的互异性可知a≠0,
所以a2≠0,-a3≠0,又A⊆B,
所以a2-1=0,解得a=±1.
当a=-1时,a2=-a3=1,这与集合元素互异性矛盾,舍去.
当a=1时,A={0,1},B={1,-1,0},满足A⊆B.
综上a=1,
故答案为:1.
点评 解出a=±1后,检验这两个值是否都满足元素的互异性的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列关于算法的说法中,正确的是( )
| A. | 算法是某个问题的解决过程 | B. | 算法执行后可以不产生确定的结果 | ||
| C. | 解决某类问题的算法不是唯一的 | D. | 算法可以无限的操作下去不停止 |
6.已知函数g(x)=$\sqrt{2{x^2}-3x+1}$,则函数g(x)的定义域为( )
| A. | (-∞,$\frac{1}{2}$]∪[2,+∞) | B. | [$\frac{1}{2}$,1] | C. | (-∞,$\frac{1}{2}$]∪[1,+∞) | D. | (-∞,-1]∪[$\frac{1}{2}$,+∞) |
13.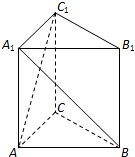 如图,三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥AB且AA1=AC=AB,则直线AC1与直线A1B所成的角等于( )
如图,三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥AB且AA1=AC=AB,则直线AC1与直线A1B所成的角等于( )
 如图,三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥AB且AA1=AC=AB,则直线AC1与直线A1B所成的角等于( )
如图,三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC⊥AB且AA1=AC=AB,则直线AC1与直线A1B所成的角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
7.定义运算(a,b)?(c,d)=ac-bd,则符合条件(z,1-2i)?(-1,1+i)=0的复数z的所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |