题目内容
若实数x、y、m满足|x-m|≤|y-m|,则称x比y更接近m.
(1)若x2-3比1更接近0,求x的取值范围;
(2)对任意两个正数a、b,试判断(
)2与
哪一个更接近ab?并说明理由;
(3)当a≥2且x≥1时,证明:
比x+a更接近lnx.
(1)若x2-3比1更接近0,求x的取值范围;
(2)对任意两个正数a、b,试判断(
| a+b |
| 2 |
| a2+b2 |
| 2 |
(3)当a≥2且x≥1时,证明:
| e |
| x |
考点:利用导数研究函数的单调性,绝对值不等式的解法
专题:计算题,新定义,不等式的解法及应用
分析:(1)由新定义可得|x2-3|≤1,由绝对值不等式的解法,即可得到解集;
(2)方法一、运用新定义作差比较,即可得到;
方法二、运用基本不等式,即可比较;
(3)令p(x)=
-lnx,q(x)=x+a-lnx,分别求出单调性,再讨论①当1≤x≤e时,②当x>e时,再由新定义作差比较即可得证.
(2)方法一、运用新定义作差比较,即可得到;
方法二、运用基本不等式,即可比较;
(3)令p(x)=
| e |
| x |
解答:
解:(1)依题意可得|x2-3|≤1?-1≤x2-3≤1?-2≤x≤-
或
≤x≤2,
∴x的取值范围为[-2,-
]∪[
,2];
(2)解法一:∵|(
)2-ab|-|
-ab|=|
2|-|
|
=
-
=-
≤0,
即|(
)2-ab|≤|
-ab|,
∴(
)2比
更接近ab;
解法二:∵对任意两个正数a、b,有(
)2≥ab,
≥ab,
∴|(
)2-ab|-|
-ab|=(
)2-
=-
≤0,
即|(
)2-ab|≤|
-ab|,
∴(
)2比
更接近ab;
(3)证明:令p(x)=
-lnx,q(x)=x+a-lnx,
则p(x)在区间[1,+∞)上单调递减,且p(e)=0,
由q′(x)=1-
=
,得当x≥1时,q'(x)≥0,
∴q(x)在[1,+∞)上单调递增,且当x≥1时,有q(x)≥q(1)=0,
①当1≤x≤e时,∵p(x)≥0,a≥2,
∴|p(x)|-|q(x)|=
-lnx-(x+a-lnx)=
-x-a≤e-1-2<0.
∴
比x+a更接近lnx.
②当x>e时,
方法一:∵p(x)<0,q(x)>0.,
∴|p(x)|-|q(x)|=lnx-
-(x+a-lnx)=2lnx-
-x-a<2lnx-x-2.
令f(x)=2lnx-x-2,则f′(x)=
-1=
.当x>e时,f'(x)<0.
∴f(x)在区间(e,+∞)单调递减,当x>e时,f(x)<f(e)=-e<0
综上可知,当x≥1时,|
-lnx|-|x+a-lnx|≤0.即|
-lnx|≤|x+a-lnx|.
∴
比x+a更接近lnx.
方法二:当x>e时,∵p(x)<0,q(x)>0.
∴|p(x)|-|q(x)|=lnx-
-(x+a-lnx)=2lnx-
-x-a,
令f(x)=2lnx-
-x-a,则f′(x)=
-1+
=-
.
令f'(x)=0,解得x1=1+
,x2=1-
,
∵x>e∴x2=1-
不合舍去,
∵(e-1)2<1+e,∴e-1<
∴x1>e
∵当e<x<x1时,f'(x)>0.当x>x1时,f'(x)<0.
∴f(x)在区间(e,x1)单调递增,在(x1,+∞)单调递减,又e<x1<3
∴当x>e时,f(x)≤f(x1)=2lnx1-
-x1-a<2ln3-e-2<0.
综上可知,当x≥1时,|
-lnx|-|x+a-lnx|≤0.即|
-lnx|≤|x+a-lnx|.
∴
比x+a更接近lnx.
| 2 |
| 2 |
∴x的取值范围为[-2,-
| 2 |
| 2 |
(2)解法一:∵|(
| a+b |
| 2 |
| a2+b2 |
| 2 |
| (a-b) |
| 4 |
| (a-b)2 |
| 2 |
=
| (a-b)2 |
| 4 |
| (a-b)2 |
| 2 |
| (a-b)2 |
| 4 |
即|(
| a+b |
| 2 |
| a2+b2 |
| 2 |
∴(
| a+b |
| 2 |
| a2+b2 |
| 2 |
解法二:∵对任意两个正数a、b,有(
| a+b |
| 2 |
| a2+b2 |
| 2 |
∴|(
| a+b |
| 2 |
| a2+b2 |
| 2 |
| a+b |
| 2 |
| a2+b2 |
| 2 |
| (a-b)2 |
| 4 |
即|(
| a+b |
| 2 |
| a2+b2 |
| 2 |
∴(
| a+b |
| 2 |
| a2+b2 |
| 2 |
(3)证明:令p(x)=
| e |
| x |
则p(x)在区间[1,+∞)上单调递减,且p(e)=0,
由q′(x)=1-
| 1 |
| x |
| x-1 |
| x |
∴q(x)在[1,+∞)上单调递增,且当x≥1时,有q(x)≥q(1)=0,
①当1≤x≤e时,∵p(x)≥0,a≥2,
∴|p(x)|-|q(x)|=
| e |
| x |
| e |
| x |
∴
| e |
| x |
②当x>e时,
方法一:∵p(x)<0,q(x)>0.,
∴|p(x)|-|q(x)|=lnx-
| e |
| x |
| e |
| x |
令f(x)=2lnx-x-2,则f′(x)=
| 2 |
| x |
| 2-x |
| x |
∴f(x)在区间(e,+∞)单调递减,当x>e时,f(x)<f(e)=-e<0
综上可知,当x≥1时,|
| e |
| x |
| e |
| x |
∴
| e |
| x |
方法二:当x>e时,∵p(x)<0,q(x)>0.
∴|p(x)|-|q(x)|=lnx-
| e |
| x |
| e |
| x |
令f(x)=2lnx-
| e |
| x |
| 2 |
| x |
| e |
| x2 |
| x2-2x-e |
| x2 |
令f'(x)=0,解得x1=1+
| 1+e |
| 1+e |
∵x>e∴x2=1-
| 1+e |
∵(e-1)2<1+e,∴e-1<
| 1+e |
∵当e<x<x1时,f'(x)>0.当x>x1时,f'(x)<0.
∴f(x)在区间(e,x1)单调递增,在(x1,+∞)单调递减,又e<x1<3
∴当x>e时,f(x)≤f(x1)=2lnx1-
| e |
| x1 |
综上可知,当x≥1时,|
| e |
| x |
| e |
| x |
∴
| e |
| x |
点评:本题考查新定义的理解和运用,考查绝对值不等式的解法和性质的运用,考查构造函数,运用导数判断单调性,进而得到两数的大小关系,属于中档题和易错题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
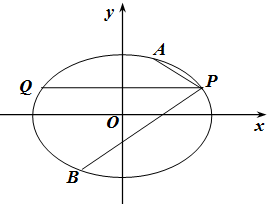 已知椭圆C的中心在原点,焦点在x轴上,离心率为
已知椭圆C的中心在原点,焦点在x轴上,离心率为