题目内容
已知集合M={α|α=k•90°-36°},N={α|-180°<α<180°},则M∩N= .
考点:交集及其运算
专题:三角函数的求值,集合
分析:分别取k=0,1,2,-1,得到M内α的值,与N取交集得答案.
解答:
解:∵M={α|α=k•90°-36°},
当k=0时α=-36°,k=1时α=54°,k=2时α=144°,k=-1时α=-126°,
又N={α|-180°<α<180°},
∴M∩N={-36°,54°,144°,-126°}.
故答案为:{-36°,54°,144°,-126°}.
当k=0时α=-36°,k=1时α=54°,k=2时α=144°,k=-1时α=-126°,
又N={α|-180°<α<180°},
∴M∩N={-36°,54°,144°,-126°}.
故答案为:{-36°,54°,144°,-126°}.
点评:本题考查了交集及其运算,考查了轴线角,是基础题.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
数列{an}的各项为正数,其前n项和Sn=4-(
)n-2(n∈N*).若Tn=a1a2+a2a3+…+anan+1(n∈N*),则Tn的取值所在的区间最恰当的是( )
| 1 |
| 2 |
A、(0,
| ||
| B、[2,4) | ||
C、[2,
| ||
| D、(0,4) |
在下列各数中,最大的数是( )
| A、11111(2) |
| B、1000(4) |
| C、210(6) |
| D、85(9) |
已知点P是椭圆
+
=1上的一点,且以点P及焦点F1,F2为顶点的三角形的面积等于1,则这样的点P有( )
| x2 |
| 5 |
| y2 |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
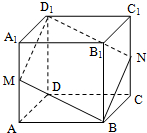 在正方体ABCD-A1B1C1D1 中,过对角线BD1 的一个平面交AA1 于M,交CC1 于N.给出下列四个结论:
在正方体ABCD-A1B1C1D1 中,过对角线BD1 的一个平面交AA1 于M,交CC1 于N.给出下列四个结论: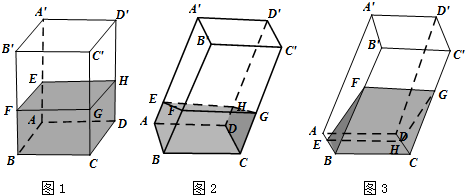
 如图,在矩形ABCD,AB=a,BC=1(a>1),点E,F,G,H分别在边AB、BC、CD、DA上,且有BE=BF=DG=DH=x
如图,在矩形ABCD,AB=a,BC=1(a>1),点E,F,G,H分别在边AB、BC、CD、DA上,且有BE=BF=DG=DH=x