题目内容
垂直于直线l1：3x-4y+100=0的直线l2，l2与两坐标轴所围成的三角形的面积为6，则直线l2在x轴上的截距为 ．
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：根据直线垂直的关系求出直线方程即可得到结论．
解答：
解：∵直线l2垂直于直线l1：3x-4y+100=0，
∴设直线l2的方程为4x+3y+b=0，
当x=0时，y=-
，
当y=0时，x=-
，
∵l2与两坐标轴所围成的三角形的面积为6，
∴
|-
|•|-
|=6，
即b2=144，解得b=12或-12，
则直线l2在x轴上的截距为x=-
=-3或3，
故答案为：-3或3
∴设直线l2的方程为4x+3y+b=0，
当x=0时，y=-
| b |
| 3 |
当y=0时，x=-
| b |
| 4 |
∵l2与两坐标轴所围成的三角形的面积为6，
∴
| 1 |
| 2 |
| b |
| 3 |
| b |
| 4 |
即b2=144，解得b=12或-12，
则直线l2在x轴上的截距为x=-
| b |
| 4 |
故答案为：-3或3
点评：本题主要考查直线方程的求解，根据直线垂直的关系设出直线方程是解决本题的关键．
练习册系列答案
相关题目
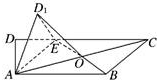如图，在梯形ABCD中，AB∥CD，∠ADC=90°，AB=2，DC=3，AD=1．E是DC上一点，且DE=1，连接AE，将△DAE沿AE折起到△D1AE的位置，使得∠D1AB=30°，设AC与BE的交点为O．