题目内容
已知函数f(x)=
x3+ax+b(a,b∈R)在x=2处取得的极小值是-
.
(1)求f(x)的单调递增区间;
(2)若x∈[-4,3]时,有f(x)=m2+m+
恒成立,求实数m的取值范围.
| 1 |
| 3 |
| 4 |
| 3 |
(1)求f(x)的单调递增区间;
(2)若x∈[-4,3]时,有f(x)=m2+m+
| 10 |
| 3 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:(1)求出函数的导数,由题意可得,f(2)=-
,f′(2)=0,解得即可得到a,b,进而通过解f′(x)>0,即可得到单调增区间;
(2)求出f(x)的导数,单调区间和极值,及在[-4,3]上的最大值,再由f(x)≤m2+m+
在[-4,3]上恒成立等价于m2+m+
≥
,解不等式即可得到.
| 4 |
| 3 |
(2)求出f(x)的导数,单调区间和极值,及在[-4,3]上的最大值,再由f(x)≤m2+m+
| 10 |
| 3 |
| 10 |
| 3 |
| 28 |
| 3 |
解答:
解:(1)f′(x)=x2+a,由题意
,解得
,
令f′(x)=x2-4>0得f(x)的单调递增区间为(-∞,-2)和(2,+∞).
(2)f(x)=
x3-4x+4,当x变化时,f′(x)与f(x)的变化情况如下表:
所以-4≤x≤3时,f(x)max=
.
于是f(x)≤m2+m+
在[-4,3]上恒成立等价于m2+m+
≥
,
求得m∈(-∞,-3]∪[2,+∞).
|
|
令f′(x)=x2-4>0得f(x)的单调递增区间为(-∞,-2)和(2,+∞).
(2)f(x)=
| 1 |
| 3 |
| x | -4 | (-4,-2) | -2 | (-2,2) | 2 | (2,3) | 3 | ||||||
| f′(x) | + | 0 | - | 0 | + | ||||||||
| f(x) | -
| 单调递增 |
| 单调递减 | -
| 单调递增 | 1 |
| 28 |
| 3 |
于是f(x)≤m2+m+
| 10 |
| 3 |
| 10 |
| 3 |
| 28 |
| 3 |
求得m∈(-∞,-3]∪[2,+∞).
点评:本题考查导数的运用:求单调区间和极值、最值,考查不等式恒成立转化为求函数的最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
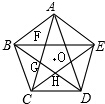 如图,求边长为1的正五边形的对角线围成的正五边形的边长.
如图,求边长为1的正五边形的对角线围成的正五边形的边长.