题目内容
命题p：“矩形的两条对角线相等”的逆命题是（ ）
| A、两条对角线相等的四边形是矩形 |
| B、矩形的两条对角线不相等 |
| C、有的矩形两条对角线不相等 |
| D、对角线不相等的四边形不是矩形 |
考点：四种命题
专题：简易逻辑
分析：命题“若p，则q”的逆命题是“若q，则p”，直接写出即可．
解答：
解：∵命题：“矩形的两条对角线相等”的
题设是“四边形是矩形”，
结论是“两条对角线相等”
∴这个命题的逆命题是：
“两条对角线相等的四边形是矩形”；
故选：A
题设是“四边形是矩形”，
结论是“两条对角线相等”
∴这个命题的逆命题是：
“两条对角线相等的四边形是矩形”；
故选：A
点评：本题考查了命题与逆命题之间的关系，是基础题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知全集U=R，集合A={1，2，3，4，5}，B=[3，+∞），则图中阴影部分所表示的集合为（ ）
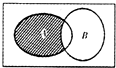
| A、{0，1，2} |
| B、{0，1} |
| C、{1，2} |
| D、{1} |
集合A={-1，0，1}，B={y|y=x2+1，x∈A}，则A∩B=（ ）
| A、{0} | B、{1} |
| C、{0，1} | D、{-1，0，1} |
已知函数g（x）是偶函数，f（x）=g（x-2），且当x≠2时其导函数f（x）满足（x-2）f′（x）＞0，若1＜a＜3，则（ ）
| A、f（4a）＜f（3）＜f（log3a） |
| B、f（3）＜f（log3a）＜f（4a） |
| C、f（log3a）＜f（3）＜f（4a） |
| D、f（log3a）＜f（4a）＜f（3） |
设a=30.3，b=log53，c=cos2，则（ ）
| A、c＜b＜a |
| B、c＜a＜b |
| C、a＜b＜c |
| D、b＜c＜a |
已知a，b∈R．下列四个条件中，使a＞b成立的必要条件是（ ）
| A、a＞b-1 |
| B、a＞b+1 |
| C、丨a丨＞丨b丨 |
| D、a-1＞b-1 |
命题p：“?x∈Z，x2≥0”，则?p为（ ）
| A、?x∈Z，x2＜0 |
| B、?x∉Z，x2＜0 |
| C、?x0∈Z，x02≥0 |
| D、?x0∈Z，x02＜0 |