题目内容
3．i为虚数单位，则$\frac{2}{1+i}$+i=1．分析 直接由复数代数形式的乘除运算化简$\frac{2}{1+i}$+i得答案．
解答 解：$\frac{2}{1+i}$+i=$\frac{2（1-i）}{（1+i）（1-i）}+i=1-i+i=1$，
故答案为：1．
点评 本题考查了复数代数形式的乘除运算，是基础题．
练习册系列答案
相关题目
13．运行如图所示的程序框图，则输出结果为（ ）
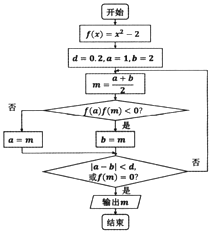
| A． | $\frac{11}{8}$ | B． | $\frac{5}{4}$ | C． | $\frac{3}{2}$ | D． | $\frac{23}{16}$ |
11．若${（x-2）^5}={a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+{a_4}{x^4}+{a_5}{x^5}$，则a1+a2+a3+a4+a5=（ ）
| A． | -1 | B． | -31 | C． | -33 | D． | 31 |
18．已知集合A={x|x-x2＜0}，B={0，1，2，3}，则（∁RA）∩B=（ ）
| A． | {0，1} | B． | {x|0≤x≤1} | C． | {2，3} | D． | {1，2，3} |
12．在△ABC中，内角A，B，C所对的边分别是a，b，c，若c2=（a-b）2+6，C=$\frac{π}{3}$，则△ABC的面积是（ ）
| A． | $\frac{3\sqrt{3}}{2}$ | B． | $\frac{9\sqrt{3}}{2}$ | C． | $\sqrt{3}$ | D． | 3$\sqrt{3}$ |
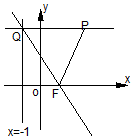如图在直角坐标系xOy中，过动点P的直线与直线l：x=-1垂直，垂足为Q，点F（1，0）满足$\overrightarrow{FP}•\overrightarrow{FQ}=\overrightarrow{QP}•\overrightarrow{QF}$．