题目内容
15.已知i是虚数单位,若复数z满足(2-i)z=3+i,则复数z为1+i.分析 把已知等式变形,然后由复数代数形式的乘除运算化简复数z得答案.
解答 解:由(2-i)z=3+i,
得$z=\frac{3+i}{2-i}=\frac{(3+i)(2+i)}{(2-i)(2+i)}=\frac{5+5i}{5}=1+i$,
故答案为:1+i.
点评 本题考查了复数代数形式的乘除运算,是基础题.

练习册系列答案
相关题目
5.设集合A={x|$\frac{2x-1}{x-2}$≤0},B={x||x|<1},则A∪B=( )
| A. | [-$\frac{1}{2}$,1) | B. | (-1,1)∪(1,2) | C. | (-1,2) | D. | [-$\frac{1}{2}$,2) |
6.下列叙述正确的是( )
| A. | 第一或第二象限的角都可作为三角形的内角 | |
| B. | 钝角比第三象限的角小 | |
| C. | 第四象限的角一定是负角 | |
| D. | 始边相同而终边不同的角一定不相等 |
7.已知抛物线C:y2=2px(p>0)上一点(5,m)到焦点的距离为6,P,Q分别为抛物线C与圆M:(x-6)2+y2=1上的动点,当|PQ|取得最小值时,向量$\overrightarrow{PQ}$在x轴正方向上的投影为( )
| A. | 2-$\frac{{\sqrt{5}}}{5}$ | B. | 2$\sqrt{5}$-1 | C. | 1-$\frac{{\sqrt{21}}}{21}$ | D. | $\sqrt{21}$-1 |
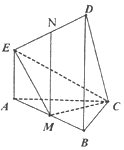 如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.
如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M,N分别为AB,DE的中点.