题目内容
12.函数f(x)=lgx-6+3x的零点x0∈(k,k+1),k∈Z,则k=1.分析 判断函数的单调性,根据函数零点的判断条件即可得到结论.
解答 解:函数f(x)=lgx-6+3x单调递增,
∵f(2)=lg2-6+6=lg2>0,
f(1)=lg1-6+3=-3<0,
∴f(1)f(2)<0,
即函数f(x)在(1,2)内存在唯一的零点,
∵函数f(x)=lgx-6+3x的零点在区间(k,k+1)上,k∈Z,
∴k=1,
故答案为:1.
点评 本题主要考查函数零点区间的判断,根据函数零点存在的条件是解决本题的关键.

练习册系列答案
相关题目
7.对空间任一点O和不共线三点A,B,C,能得到P,A,B,C四点共面的是( )
| A. | $\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{OP}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{OP}$=-$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$+$\frac{1}{2}$$\overrightarrow{OC}$ | D. | 以上皆错 |
4.一个几何体的三视图,则该几何体的体积为( )
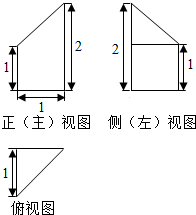

| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | 2 |
6.如图,在四形边ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使CD⊥平面ABD,构成三棱锥A-BCD.则在三棱锥A-BCD中,下列结论正确的是( )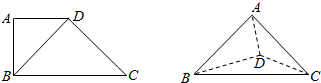

| A. | AD⊥平面BCD | B. | AB⊥平面BCD | C. | 平面BCD⊥平面ABC | D. | 平面ADC⊥平面ABC |