题目内容
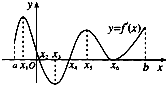
设函数y=f（x），x∈[a，b]，其导函数的图象如图所示，则函数y=f（x）的减区间是（ ）
| A、（x1，x3） |
| B、（x2，x4） |
| C、（x4，x6） |
| D、（x5，x6） |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：通过图象得出导函数的正负，从而得出函数f（x）的单调性，进而得出答案．
解答：
解：由图象得：在（x2，x4）上，f′（x）＜0，
∴函数y=f（x）的减区间是：（x2，x4），
故选：B．
∴函数y=f（x）的减区间是：（x2，x4），
故选：B．
点评：本题考查了函数的单调性，导数的应用，考查读图的能力，是一道基础题．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
函数y=2-|x-1|-m的图象与x轴有交点时，m的范围是（ ）
| A、-1≤m＜0 | B、0≤m≤1 |
| C、m≥1 | D、0＜m≤1 |
下列计算正确的是（ ）
| A、3-1=3 | ||||
B、tan30°=
| ||||
| C、π0=1π | ||||
| D、|-a3|2=a5 |