题目内容
设A,B是两个非空集合,定义A与B的差集A-B={x|x∈A,且x∉B}.
(1)试举出两个数集,求它们的差集;
(2)差集A-B与B-A是否一定相等?说明理由;
(3)已知A={x|x>4},B={x|-6<x<6},求A-(A-B)和B-(B-A).
(1)试举出两个数集,求它们的差集;
(2)差集A-B与B-A是否一定相等?说明理由;
(3)已知A={x|x>4},B={x|-6<x<6},求A-(A-B)和B-(B-A).
考点:交、并、补集的混合运算
专题:集合
分析:利用差集定义和不等式性质求解.
解答:
解:(1)如A={1,2,3},B={2,3,4},
则A-B={1}.
(2)不一定相等,
由(1)B-A={4},而A-B={1},
故A-B≠B-A.
又如,A=B={1,2,3}时,
A-B=∅,B-A=∅,此时A-B=B-A,
故A-B与B-A不一定相等.
(3)因为A-B={x|x≥6},
B-A={x|-6<x≤4},
A-(A-B)={x|4<x<6},
B-(B-A)={x|4<x<6}.
则A-B={1}.
(2)不一定相等,
由(1)B-A={4},而A-B={1},
故A-B≠B-A.
又如,A=B={1,2,3}时,
A-B=∅,B-A=∅,此时A-B=B-A,
故A-B与B-A不一定相等.
(3)因为A-B={x|x≥6},
B-A={x|-6<x≤4},
A-(A-B)={x|4<x<6},
B-(B-A)={x|4<x<6}.
点评:本题考查差集的定义及应用,解题时要认真审题,是基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
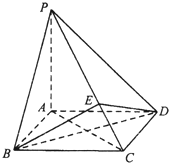 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PA=AD=1,PA⊥面ABCD,E为线段PC上靠近D的一个三等分点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PA=AD=1,PA⊥面ABCD,E为线段PC上靠近D的一个三等分点.