题目内容
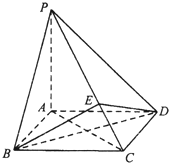 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PA=AD=1,PA⊥面ABCD,E为线段PC上靠近D的一个三等分点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PA=AD=1,PA⊥面ABCD,E为线段PC上靠近D的一个三等分点.(1)证明:PC⊥面BDE;
(2)求三棱锥P-BED的体积V.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)先证明OE⊥PC,由PA⊥平面ABC,由线面垂直的性质可得PA⊥BD,进而由线面垂直的判定定理得到PC⊥平面BDE;
(2)利用VP-BED=VP-BCD-VE-BCD,可得结论.
(2)利用VP-BED=VP-BCD-VE-BCD,可得结论.
解答:
(1)证明:设AC∩BD=O,连接OE,
根据题意,△PAC中,PA=1,AC=
,PC=
,则EC=
,OC=
,
∴
=
=
,∠ECO=∠ACP,
∴△ECO∽△ACP,
∴OE⊥PC,
∵PA⊥平面ABC,又BD?平面ABC
∴PA⊥BD,∵AC⊥BD,又AP∩AC=A
∴BD⊥平面PAC,又PC?平面PAC,
∴BD⊥PC,又BE∩BD=B,∴PC⊥平面BDE;
(2)解:∵E为线段PC上靠近D的一个三等分点,
∴E到底面ABCD的距离为
,
∴VE-BCD=
×
×1×1×
=
,
∵VP-BCD=
×
×1×1×1=
,
∴VP-BED=VP-BCD-VE-BCD=
-
=
.
根据题意,△PAC中,PA=1,AC=
| 2 |
| 3 |
| ||
| 3 |
| ||
| 2 |
∴
| EC |
| OC |
| AC |
| PC |
| ||
| 3 |
∴△ECO∽△ACP,
∴OE⊥PC,
∵PA⊥平面ABC,又BD?平面ABC
∴PA⊥BD,∵AC⊥BD,又AP∩AC=A
∴BD⊥平面PAC,又PC?平面PAC,
∴BD⊥PC,又BE∩BD=B,∴PC⊥平面BDE;
(2)解:∵E为线段PC上靠近D的一个三等分点,
∴E到底面ABCD的距离为
| 1 |
| 3 |
∴VE-BCD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 18 |
∵VP-BCD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴VP-BED=VP-BCD-VE-BCD=
| 1 |
| 6 |
| 1 |
| 18 |
| 1 |
| 9 |
点评:熟练掌握线线,线面垂直之间的转化关系,掌握锥体的体积公式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在三棱柱ABC-A1B1C1中,侧棱BB1⊥底面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC中点.
如图,在三棱柱ABC-A1B1C1中,侧棱BB1⊥底面ABC,∠BAC=90°,AB=AC=AA1=2,且E是BC中点.