题目内容

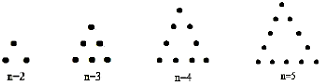
如图所示，将若干个点摆成三角形图案，每条边（包括两个端点）有n（n＞1，n∈N*）个点，相应的图案中总的点数记为an，按上述规律，则a6=
 
，an=
 
．
考点：归纳推理
专题：推理和证明
分析：根据已知的图形中点的个数得出变化规律进而求出即可．
解答： 解：∵第一图形中有3×2-3=3个点，
第二个图形中有3×3-3=6个点，
第三个图形中有4×3-3=9个点
…
∴an=3n-3，
a6=3×6-3=15，
故答案为：15，3n-3
点评：此题主要考查了图形的变化类，根据已知的图形中点数的变化得出规律是解题关键．
练习册系列答案
相关题目
“中国式过马路”存在很大的交通安全隐患．某调查机构为了解路人对“中国式过马路”的态度是否与性别有关，从马路旁随机抽取30名路人进行了问卷调查，得到了如下列联表：
男性 女性 合计
反感 10
不反感 8
合计 30
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
8
15
．
（1）请将上面的列联表补充完整（在答题卷上直接填写结果，不需要写求解过程）；
（2）据此资料判断是否有95%的把握认为反感“中国式过马路”与性别有关？
在直角坐标系xOy中，曲线l的参数方程为
x=t
y=3+t
（t为参数）；以原点O为极点，以x轴的正半轴为极轴建立极坐标系ρOθ，则曲线l的极坐标方程为
 
．
已知两点A（9，4）和B（3，6），则以AB为直径的圆的方程为
 
．
过P（2，0）作倾斜角为α的直线l与曲线E：
x=cosθ
y=
2
2
sinθ
（θ为参数）交于A，B两点．
（Ⅰ）求曲线E的普通方程及l的参数方程；
（Ⅱ）求sinα的取值范围．
已知向量
a
=（ex，-1），向量
b
=（1，x+1），设函数f（x）=
a
•
b
，则函数f（x）的零点个数为
 
．
已知圆的方程为x2+y2=4，圆的弦|AB|=2
3
，设A（x1，y1）、B（x2，y2），则x1x2+y1y2=
 
．
在直角坐标系xoy中，直线l的参数方程为
x=3-2t
y=-1-4t
（t为参数），若以直角坐标系xoy的O点为极点，ox为极轴，且长度单位相同，建立极坐标系，得曲线C的极坐标方程为ρ2（cos2θ-sin2θ）=16．若直线l与曲线C交于A，B两点，则AB=
 
．
某化工厂为预测产品的回收率y，需要研究它和原料有效成分含量x之间的相关关系，现取8对观测值，计算得：
8
i=1
xi=52，
8
i=1
yi=228，
8
i=1
xi2=478，
8
i=1
xiyi=1849，则y与x之间的回归直线方程是（　　）
A、
y
=11.47+2.62x
B、
y
=-11.47+2.62x
C、
y
=2.62+11.47x
D、
y
=11.47-2.62x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网