题目内容
9.若函数f(x)=ax2-bx+1(a≠0)是定义在R上的偶函数,则函数g(x)=ax3+bx2+x(x∈R)是( )| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
分析 由f(x)为偶函数容易得出b=0,从而得出g(x)=ax3+x,这样判断g(x)的奇偶性即可.
解答 解:f(x)为偶函数,则b=0;
∴g(x)=ax3+x;
∴g(-x)=a(-x)3-x=-(ax3+x)=-g(x);
∴g(x)是奇函数.
故选A.
点评 考查奇函数、偶函数的定义,以及奇函数的判断方法.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
17.一个棱长为$6\sqrt{2}$的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体棱长的最大值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
14.已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递减,若实数a满足f(3|2a+1|)>f(-$\sqrt{3}$),则a的取值范围是( )
| A. | (-∞,-$\frac{3}{4}$)∪(-$\frac{1}{4}$,+∞) | B. | (-∞,-$\frac{3}{4}$) | C. | (-$\frac{1}{4}$,+∞) | D. | (-$\frac{3}{4}$,-$\frac{1}{4}$) |
18.10、(文)若关于x的不等式x3-3x+3+a≤0恒成立,其中-2≤x≤3,则实数a的最大值为( )
| A. | 1 | B. | -1 | C. | -5 | D. | -21 |
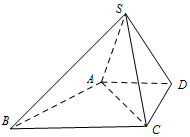 如图,在底面为直角梯形的四棱锥S-ABCD中,且AD∥BC,AD=DC=1,$SA=SC=SD=\sqrt{2}$.
如图,在底面为直角梯形的四棱锥S-ABCD中,且AD∥BC,AD=DC=1,$SA=SC=SD=\sqrt{2}$. =_________
=_________