题目内容

4．在△ABC中，若AB=8，AC=6，O为△ABC的外心，则$\overrightarrow{AO}$•$\overrightarrow{BC}$=（　　）
A．-28B．-14C．0D．16

分析 设外接圆的半径为r，由向量的三角形法则，以及向量的数量积的定义，结合等腰三角形的性质，即可得到．

解答 解：设圆的半径为r，∠AOB为α，∠AOC为β，则
AB2=AO2+BO2-2AO×BOcosα=2r2-2r2 cosα，AC2=AO2+CO2-2AO×COcosβ=2r2-2r2cosβ，
$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\overrightarrow{AO}$•（$\overrightarrow{BO}$+$\overrightarrow{OC}$）=$\overrightarrow{AO}•\overrightarrow{BO}$+$\overrightarrow{AO}$•$\overrightarrow{OC}$=r2 cosα-r2cosβ=$\frac{1}{2}$（AC2-AB2）=-14
故选B．

点评 本题考查向量的数量积的定义和性质，考查运算能力，属于中档题和易错题．

练习册系列答案
相关题目
13．已知a，b∈R，且a＜b，若aeb=bea（为自然对数的底数），则下列正确的是（　　）
A．a＜-1，-1＜b＜0B．1＜a＜2，b＞2C．0＜a＜1，b＞1D．0$＜a＜\frac{1}{e}$，b$＜\frac{1}{e}$
15．判断函数$f（x）=\frac{1}{{{x^2}+1}}$在区间（0，1）上的单调性，并用定义证明．
12．设集合{x|x2-3x-4＜0}，N={-2，-1，0，1，2}，则 M∩N=（　　）
A．{-1，0}B．{-2，-1，0}C．{0，1}D．{0，1，2}
19．已知$\overrightarrow{a}$=（3，2），$\overrightarrow{b}$=（0，-1），则|-2$\overrightarrow{a}$+4$\overrightarrow{b}$|等于10．
9．下面给出从A到B的对应f：
①A=R，B=R，f：x→$\frac{1}{x}$；②A=B={（x，y）|x∈R，y∈R}，f：（x，y）→（x+y，x-y）}③A={x|x是平面上的圆}，B={x1x是平面上的正方形}，f：画圆的内接正方形．④A={x|x是平面上的线段}，B={x|x是平面上的点}，f：取线段的中点}⑤A={x|0＜x＜1}，B={x|0＜x＜2}，f：x→3x．其中f是A到B的映射的个数为（　　）
A．1B．2C．3D．4
16．若函数y=$\frac{x}{x-m}$在区间（1，+∞）内是减函数，则实数m的取值范围是（0，1]．
14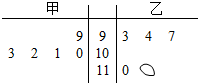．甲、乙两同学用茎叶图记录高三前5次数学测试的成绩，如图所示．他们在分析对比成绩变化时，发现乙同学成绩的一个数字看不清楚了，若已知乙的平均成绩低于甲的平均成绩，则看不清楚的数字为（　　）
A．0B．3C．6D．9
15．执行下图中的程序，如果输出的结果是4，那么输入的只可能是（　　）
A．2B．-4C．2或-4D．±2或-4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网