题目内容
12.设函数f(x)=ax+3-|2x-1|.(Ⅰ)若a=1,解不等式f(x)≤2;
(Ⅱ)若函数有最大值,求a的取值范围.
分析 (Ⅰ)需要去掉绝对值,得到不等式解得即可,
(Ⅱ)把含所有绝对值的函数,化为分段函数,再根据函数f(x)有最大值的充要条件,即可求得
解答 解:(Ⅰ)由题意得x≥$\frac{1}{2}$时,不等式化为x+3-3x+1≤2,
解得:x≥2,
x<$\frac{1}{2}$时,不等式化为x+3+2x-1≤2,解得:x≤0,
综上,不等式的解集是(-∞,0]∪[2,+∞);
(Ⅱ)由题意得f(x)=$\left\{\begin{array}{l}{(a+2)x+2,x<\frac{1}{2}}\\{(a-2)x+4,x≥\frac{1}{2}}\end{array}\right.$,
函数有最大值的充要条件是a+2≥0且a-2≤0,
即-2≤a≤2.
点评 本题主要考查含有绝对值不等式的解法,关键是去绝对值,需要分类讨论,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
20.已知i是虚数单位,则复数$\frac{{{{({1-i})}^2}}}{1+i}$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
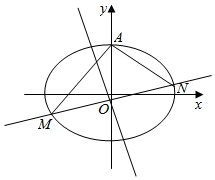 已知中心在原点O,焦点在x轴上的椭圆的一个顶点坐标为(2,0),离心率为$\frac{\sqrt{3}}{2}$
已知中心在原点O,焦点在x轴上的椭圆的一个顶点坐标为(2,0),离心率为$\frac{\sqrt{3}}{2}$