题目内容
2.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”则该人最后一天走的路程为( )| A. | 24里 | B. | 12里 | C. | 6里 | D. | 3里 |
分析 由题意可知,每天走的路程里数构成以$\frac{1}{2}$为公比的等比数列,由S6=378求得首项,再由等比数列的通项公式求得该人最后一天走的路程.
解答 解:记每天走的路程里数为{an},可知{an}是公比$q=\frac{1}{2}$的等比数列,
由S6=378,得${S}_{6}=\frac{{a}_{1}(1-\frac{1}{{2}^{6}})}{1-\frac{1}{2}}=378$,解得:a1=192,
∴${a_6}=192×\frac{1}{2^5}=6$,
故选:C.
点评 本题考查等比数列的通项公式,考查了等比数列的前n项和,是基础的计算题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列式子恒成立的是( )
| A. | sin(α+β)=sinα+sinβ | B. | cos(α-β)=cosαcosβ+sinαsinβ | ||
| C. | sin(α-β)=cosαcosβ-sinαsinβ | D. | cos(α+β)=cosαsinβ-sinαcosβ |
17.已知向量$\overrightarrow{{A}{B}}$、$\overrightarrow{{A}C}$、$\overrightarrow{{A}D}$满足$\overrightarrow{{A}C}=\overrightarrow{{A}{B}}+\overrightarrow{{A}D}$,$|{\overrightarrow{{A}{B}}}|=2$,$|{\overrightarrow{{A}D}}|=1$,E、F分别是线段BC、CD的中点.若$\overrightarrow{D{E}}•\overrightarrow{{B}F}=-\frac{5}{4}$,则向量$\overrightarrow{{A}{B}}$与向量$\overrightarrow{{A}D}$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
14.cos420°+sin330°等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 0 |
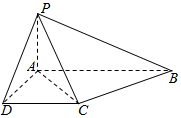 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求:
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求: