题目内容
1.若“?x∈[-$\frac{π}{4}$,$\frac{π}{4}$],m≤tanx+1”为真命题,则实数m的最大值为0.分析 求出正切函数的最大值,即可得到m的范围.
解答 解:“?x∈[-$\frac{π}{4}$,$\frac{π}{4}$],m≤tanx+1”为真命题,
可得-1≤tanx≤1,
∴0≤tanx+1≤2,
实数m的最大值为:0
故答案为:0.
点评 本题考查函数的最值的应用,命题的真假的应用,考查计算能力.

练习册系列答案
相关题目
9.若集合A={0,1,2,4},B={1,2,3},则A∪B=( )
| A. | {1,2} | B. | {0,3,4} | C. | {0,1,2,3,4} | D. | {0,1,1,2,2,3,4} |
16.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且a=1,b=2,c=$\sqrt{7}$,则∠C=( )
| A. | 120° | B. | 60° | C. | 45° | D. | 30° |
6.设等比数列{an}的前n项和为Sn,若S5、S4、S6成等差数列.则数列{an}的公比为q的值等于( )
| A. | -2或1 | B. | -1或2 | C. | -2 | D. | 1 |
13.下列式子恒成立的是( )
| A. | sin(α+β)=sinα+sinβ | B. | cos(α-β)=cosαcosβ+sinαsinβ | ||
| C. | sin(α-β)=cosαcosβ-sinαsinβ | D. | cos(α+β)=cosαsinβ-sinαcosβ |
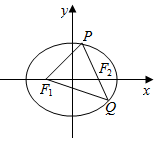 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$.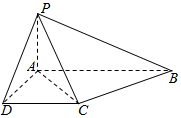 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求:
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AB∥CD,且PA=AD=CD=a,AB=2a.求: